Poligonul de tragere este un teren special amenajat în cadrul căruia se fac exerciţii şi se execută trageri cu arme de foc. Comandantul plasează câte o ţintă în toate punctele aflate la distanţele , faţă de punctul de tragere (origine) şi care au coordonatele carteziene numai numere naturale nenule.
Specialiştii în armament români au creat recent o nouă armă sub forma unui tun laser care îşi lansează razele pe o traiectorie rectilinie şi are capacitatea de a distruge toate ţintele aflate pe direcţia de tragere.
Cerință
Ştiind că tunul laser se găseşte în originea sistemului de coordonate, să se scrie un program care să determine:
- numărul de ţinte
- numărul minim de lovituri de tun laser necesare pentru a distruge toate ţintele precum
- numărul de ţinte doborâte la fiecare lovitură
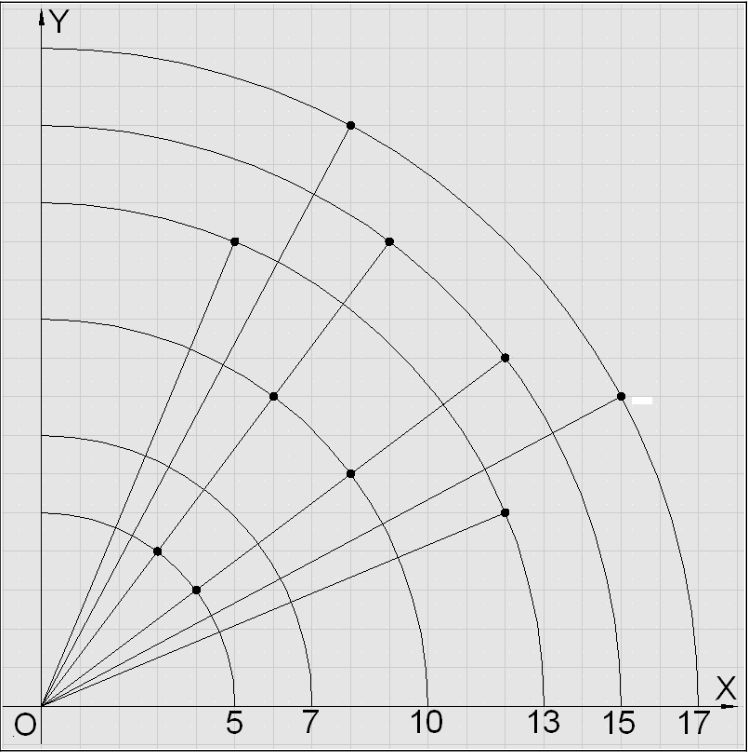
Spre exemplu, dacă avem distanţe () pentru care se încearcă plasarea ţintelor, atunci în poligon se vor plasa ţinte, va fi nevoie de lovituri pentru a doborî toate ţintele iar la fiecare lovitură se vor doborî respectiv ţinte.
Date de intrare
Fişierul de intrare poligon.in conţine pe prima linie numărul de distanţe la care vor fi plasate ţinte, iar pe a doua linie numere naturale nenule distincte separate printr-un spaţiu, ce reprezintă aceste distanţe.
Date de ieșire
Fişierul de ieşire poligon.out va conţine linii. Pe prima linie se va scrie numărul ţintelor plasate în poligon. Pe a doua linie se va scrie numărul minim de lovituri de tun laser cu care se pot doborî toate ţintele, iar pe a treia linie se va scrie numărul de ţinte doborâte la fiecare lovitură, separate printr-un spaţiu, în ordinea crescătoare a unghiurilor direcţiilor cu axa .
Restricții și precizări
- pentru fiecare set de date de intrare, în poligon va exista cel puţin o ţintă
| # | Punctaj | Restricții |
|---|---|---|
| 1 | % | pentru determinarea corectă a numărului de ţinte |
| 2 | % | determinarea corectă a numărului minim de lovituri |
| 3 | % | determinarea corectă a numărului de ţinte doborâte la fiecare lovitură |
Exemplu
poligon.in
6
5 10 15 7 13 17
poligon.out
10
6
1 1 3 3 1 1
Explicație
Avem distante:
În poligon vor fi plasate ţinte (punctele negre marcate pe figură) care pot fi doborâte din lovituri iar la fiecare lovitură se vor doborî câte ţinte.