cuburi

Pe o masă, sunt așezate unul lângă altul, $N$ cuburi numerotate în ordine cu valori de la $1$ la $N$, care au dimensiunea laturii exprimată în centimetri, printr-un număr natural nenul. Un robot inteligent este programat să construiască turnuri prin aşezarea cuburilor unul peste altul. El se află în faţa mesei de lucru, analizează în ordine fiecare cub, de la primul la ultimul, şi procedează astfel:

• dacă este la primul cub, îl lasă la locul lui pe masă;
• aşează cubul numerotat cu $K$ peste cubul numerotat cu $K-1$ doar dacă el are latura strict mai mică decât cubul $K-1$. Această operaţie se efectuează în cazul în care cubul $K-1$ se află deja într-un turn construit anterior sau dacă el a rămas pe masă. În cazul în care cubul $K$ nu poate fi aşezat peste cubul $K-1$, el rămâne la locul lui pe masă.

Cerință

Ştiind că un turn poate fi format din cel puţin un cub, scrieţi un program care să determine:

1. cel mai mare număr de cuburi alăturate care au laturile exprimate printr-un număr par de centimetri;
2. înălţimea (exprimată în centimetri) celui mai înalt turn construit de robot.

Date de intrare

De la tastatură se citesc două numere naturale $C$ și $N$, în această ordine. $C$ reprezintă numărul cerinţei şi poate avea două valori $1$ sau $2$ iar $N$ reprezintă numărul cuburilor de pe masa de lucru. Se citesc apoi $N$ numere naturale ce reprezintă lungimile laturilor cuburilor, în ordinea numerotării acestora.

Date de ieșire

Pe ecran se va afișa un singur număr natural corespunzător rezultatului obținut pentru rezolvarea fiecărei cerințe.

Restricții și precizări

• $1 \leq N \leq 10 \ 000$
• latura unui cub poate fi de la $1$ la $500 \ 000$
• există cel puțin un cub care are latura exprimată printr-un număr par de centimetri
• pentru rezolvarea corectă a primei cerințe se acordă $30$ de puncte, pentru rezolvarea corectă a celei de-a doua cerințe se acordă $70$ de puncte.

Exemplul 1

stdin

1
7
18
12
10
17
8
2
7

stdout

3

Explicație

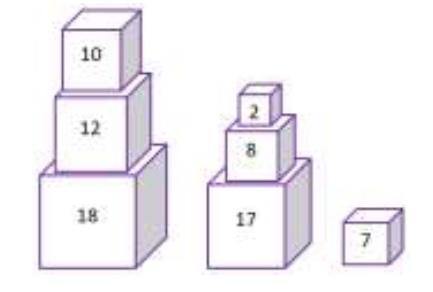
Se va rezolva cerința $1$. Sunt $7$ cuburi, așezate ca în desen. Cel mai mare număr de cuburi alăturate cu laturi exprimate printr-un număr par de centimetri este $3$.

Exemplul 2

stdin

2
7
18
12
10
17
8
2
7

stdout

40

Explicație

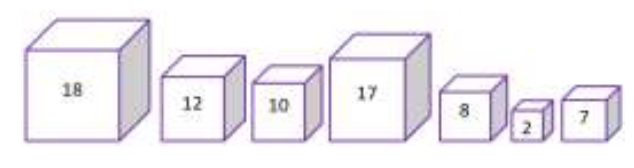
Se va rezolva cerința $2$. Se pot construi $3$ turnuri, așa cum se vede în imagine. Primul turn are înălțimea $40$ cm, al doilea $27$ cm iar cel de-al treilea $7$ cm.