fractal

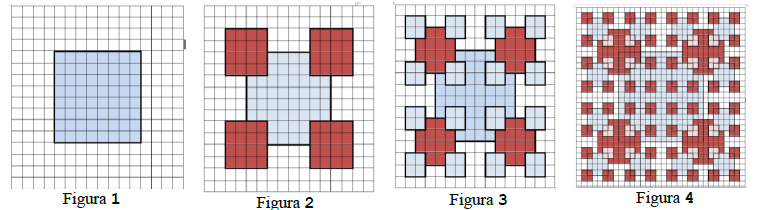
Andra este o fetiță pasionată de desen. Pentru a-și îmbunătăți performanțele școlare la geometrie, Andra îmbină pasiunea pentru desen cu rezolvarea problemelor de geometrie. Astfel, pe o foaie de matematică împărțită în pătrățele dispuse pe $2^N$ linii şi $2^N$ coloane, Andra desenează în centru o figură de forma unui pătrat de latură $2^{N-1}$ (figura $1$). Pentru fiecare colț al figurii, Andra desenează alte $4$ noi figuri cu latura egală cu jumătate din latura figurii inițiale (Figura $2$). Repetă procedeul de desenare pentru fiecare nouă figură obținută, până când ajunge la marginea foii de hârtie, fără a depăși marginile acesteia. Fiecare pătrățel care face parte dintr-o figură desenată este colorat, pentru a se distinge pe foaia de hârtie. Fiecare figură desenată este un pătrat cu laturile paralele cu marginile foii de hârtie.

Cerinţă

Scrieţi un program care citește numărul $N$, corespunzător dimensiunii de $2^N\cdot 2^N$ a foii de desen şi determină:

1. Numărul de figuri de latură minimă desenate;
2. Numărul total de pătrățele colorate cel puțin o dată de pe foaia de hârtie.

Date de intrare

Fişierul de intare fractal.in conţine pe prima linie numărul natural $C$ reprezentând cerința din problemă care trebuie rezolvată ($1$ sau $2$) și pe a doua linie, un număr natural $N$ cu semnificația de mai sus.

Date de ieşire

Dacă valoarea lui $C$ este $1$, fişierul de ieşire fractal.out va conţine un număr natural care reprezintă numărul de figuri de latură minimă. Dacă valoarea lui $C$ este $2$, fişierul de ieşire fractal.out va conţine un număr natural care reprezintă numărul total de pătrățele colorate cel puțin o dată de pe foaia de hârtie.

Restricții și precizări

• $1 < N \leq 10 \ 000$
• Pentru $30\%$ dintre teste $N \leq 30$
• Pentru rezolvarea corectă a cerinţei $1$ se obțin $30$ de puncte, iar pentru rezolvarea corectă a cerinţei $2$ se obțin $70$ de puncte.

Exemplul 1

fractal.in

1
4

fractal.out

16

Explicație

Suprafața de desen are $16$ linii și $16$ coloane (figura $3$). Pornind de la figura inițială se vor desena mai întâi $4$ figuri, apoi $16$ figuri.

Exemplul 2

fractal.in

1
5

fractal.out

64

Explicație

Suprafața de desen are $32$ linii și $32$ coloane (figura $4$). Pornind de la figura inițială se vor desena mai întâi $4$ figuri, apoi $16$ figuri, respectiv $64$ figuri de latură minimă.

Exemplul 3

fractal.in

2
4

fractal.out

148

Explicație

Suprafața desenată este cea din figura $3$. Numărul de pătrățele colorate cel puțin o dată este de $148$ din totalul de $256$ de pătrățele.

Exemplul 4

fractal.in

2
5

fractal.out

700

Explicație

Suprafața desenată este cea din figura $4$. Numărul de pătrățele colorate cel puțin o dată este de $700$ din totalul de $1 \ 024$ de pătrățele.