zmax

Se consideră o matrice cu $M$ linii și $N$ coloane. În fiecare celulă (element) a matricei este memorat câte un număr întreg. Numim „Z” o mulțime de celule din matrice formată dintr-un grup de celule consecutive, situate pe aceeași linie, legate printr-un șir de celule, situate în diagonală (pe direcția Nord-Est -> Sud-Vest), de un alt grup de celule consecutive situate pe o altă linie a matricei, neadiacentă (neconsecutivă) cu prima linie (adică între linia de sus și cea de jos a unui “Z” să mai existe cel puțin încă o linie a matricei).
Un astfel de „Z” îndeplinește condițiile:

• fiecare dintre cele două linii orizontale ale „Z”-ului are cel puțin două celule;
• diagonala începe cu celula cea mai din dreapta a liniei de sus a „Z”-ului, fiecare dintre celulele următoare se află imediat în stânga și în jos față de cea anterioară, ultima celulă a diagonalei este cea mai din stânga celulă a liniei de jos a „Z”-ului.

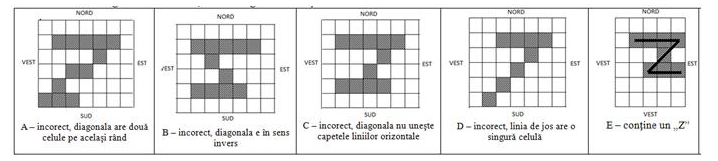
Dintre imaginile următoare, doar imaginea E conține un „Z”:

Asociem fiecărui astfel de „Z” un cost egal cu suma numerelor memorate în celulele care alcătuiesc „Z”-ul.

Cerință

Scrieți un program care să citească numerele naturale $M$ și $N$, cele $M \times N$ numere memorate în celulele matricei și să determine cel mai mare cost al unui „Z” din matrice.

Date de intrare

Fișierul de intrare zmax.in conține pe prima linie numerele naturale $M$ și $N$, separate printr-un spațiu. Pe fiecare dintre următoarele $M$ linii se găsesc câte $N$ numere întregi, separate de câte un spațiu.

Date de ieșire

Fișierul de ieșire zmax.out va conține pe prima linie un singur număr întreg reprezentând cel mai mare cost al unui „Z” din matrice.

Restricții și precizări

• $3 \leq M, N \leq 500$;
• Numerele memorate în celulele matricei sunt numere întregi din intervalul închis [$-10 \ 000$, $10 \ 000$].

Exemplu

zmax.in

5 4
3 -5 -2 4
-2 7 1 -3
1 1 1 1
2 -3 2 -3
3 -2 1 -4

zmax.out

10

Explicație

3 -5 -2 4
-2 7 1 -3
1 1 1 1
2 -3 2 -3
3 -2 1 -4

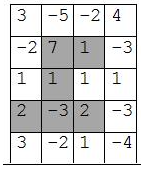
Matricea are $5$ linii și $4$ coloane și conținutul din imaginea alăturată.
Cel mai mare cost care poate fi asociat unui „Z” din matrice („Z” -ul din imagine) este $10$.