masina

Se știe că Balaurul este un împătimit al volanului. Ieri a ajuns la o intersecție (daca îi putem zice așa) foarte ciudată, ca în figura alăturată …



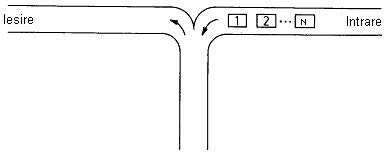
La această intersecție au ajuns N mașini (numerotate de la 1 la N). Balaurul se află în mașina X. În momentul acela se întrecea cu mașina Y (X diferit de Y). Cele 3 drumuri sunt foarte înguste, așa încât doar o mașină poate să încapă, deci depășirea este imposibilă. Totuși, datorită configurației drumurilor, mașinile își pot schimba poziția la ieșire.

De exemplu, pentru N = 3, la final avem 5 posibilități de ordonare a celor 3 mașini :

1. 1 2 3 : intră mașina 1 pe drumul din mijloc, și iese 1, intră 2 și iese 2, intră 3 și iese 3
2. 1 3 2 : intră 1 și iese 1, intra 2, intra 3, iese 3, iese 2
3. 2 1 3 : intră 1, intră 2, iese 2, iese 1, intră 3, iese 3
4. 2 3 1 : intră 1, intră 2, iese 2, intră 3, iese 3, iese 1
5. 3 2 1 : intră 1, intră 2, intră 3, iese 3, iese 2, iese 1

Oricare din cele M (în cazul acesta N = 3, M = 5) configurații posibile are șanse egale de a se întâmpla.

Balaurul vrea să știe care sunt șansele (în procente) ca la final să iasă în fața mașinii cu care se întrecea.

Cerința

Ajutați-l pe Balaur să determine șansele de a câștiga, deci de a ieși în fața mașinii Y.

Date de intrare

Pe prima linie a fișierului masina.in se află 3 numere naturale N, X si Y, separate prin câte un spatiu, reprezentând numărul de mașini, mașina Balaurului și respectiv mașina concurentului.

Date de ieșire

Fișierul masina.out va conține pe singura sa linie un singur număr real cu primele 2 zecimale exacte (obținute prin trunchiere), și anume șansele (în procente) ca Balaurul să iasă la final în fața concurentului.

Restricții și precizări

• 1 < N < 101
• 0 < X,Y < N+1
• pentru 50% din teste X=1
• trunchierea la două zecimale exacte a numărului real 60.5673 este 60.56
• trunchierea la două zecimale exacte a numărului real 60.5628 este 60.56
• trunchierea la două zecimale exacte a numărului real 60.5655 este 60.56

Exemplu

masina.in

3 1 3

masina.out

60.00

Explicație

Din cele 5 configurații în total, în 3 dintre ele mașina 1 iese în fața mașinii 3, deci șansele sunt de 60%