As a pastime, Luca likes to play “Connect the dots”, a game that requires you to connect all the given points with a line, effectively revealing a figure’s outline.
While looking at the lines that connect the dots, Luca is wondering what would happen if those had an arrow (i.e., they would not only just connect two dots, but they would always have a direction). Even though it is entirely useless for the game, Luca is nonetheless curious about the potential reveal of some interesting patterns.
When the arrows are added in certain ways, some dots might become stars: either all the connections in which they are involved have an arrow that starts from them and leads elsewhere, or they all point towards that dot.
Here is an example: the left figure is the original one, the middle and the right ones are the result of two out of the many ways to add arrows. The dots highlighted in red and blue are two examples of, respectively, the former and the latter kind of stars.
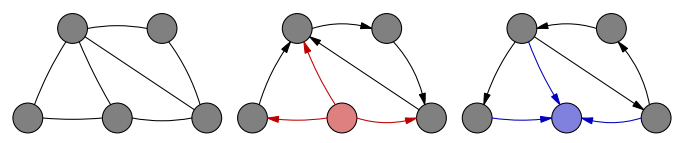
Can you come up with a way to add an arrow to (i.e, direct) every connection between two dots such that the result does not contain any star?
Input data
The first line contains two integers and , respectively the number of dots and the number of connections between them. The following lines contain two integers and each, indicating that the two dots are connected with a line.
Output data
You need to write lines, each containing two integers , to indicate a directed arrow starting from and ending in . You can print the lines in any order.
Constraints and clarifications
- ;
- ;
- , ;
- Each dot is connected to at least one line.
- It is guaranteed that at least one solution exists. In case of multiple solutions, you can output any.
| # | Score | Constraints |
|---|---|---|
| 1 | 0 | Examples. |
| 2 | 20 | The connections form a cycle, as in the first sample case. |
| 3 | 30 | |
| 4 | 50 | No additional limitations. |
Example 1
stdin
4 4
1 0
3 1
2 3
2 0
stdout
0 1
1 3
3 2
2 0
Explanation
The following is a possible solution for the first sample case:
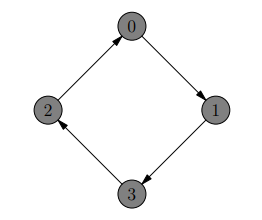
Example 2
stdin
5 7
0 1
1 2
0 3
3 1
3 2
3 4
4 2
stdout
0 1
1 2
2 3
2 4
3 0
3 1
4 3
Explanation
The second sample case corresponds to the one described earlier in the statement. The solution avoids the formation of any kind of star.