Giorgio and Edoardo are planning to go on a tour of Venice, and they are particularly interested in Murano’s famous colored Venetian glass.

There are shops which sell glasswares and they are numbered from to , the -th shop sells only pieces of color . Giorgio and Edoardo are interested in visiting some shop and buying some glasswares, they will be happy if they have bought glasswares of at least different colors.
The fastest (and the only one) way to travel in Murano is by gondola, in particular there are gondolas, each gondola can carry Giorgio and Edoardo from shop to and viceversa. However, gondolas are not free and each trip requires a ticket (each ticket is valid for one trip only, so taking the same gondola twice requires two tickets).
Giorgio and Edoardo can start and finish the tour in any shop, help them find the minimum number of tickets required to buy at least glasswares of different colors, or tell that they can’t.
Input data
The first line contains the integers and , the number of shops and the number of available gondolas. The second line contains integers, for = .
The following lines contain integers and each, meaning that a gondola can travel between shops and .
Output data
You need to write a single line with an integer: the minimum number of tickets Giorgio and Edoardo need or if they can’t visit shops with glasswares of different colors.
Constraints and clarifications
- ;
- ;
- ;
- , ;
| # | Score | Constraints |
|---|---|---|
| 1 | 0 | Examples |
| 2 | 20 | |
| 3 | 20 | |
| 4 | 20 | For each = , there are at most two values of for which = or = . |
| 5 | 40 | No additional limitations. |
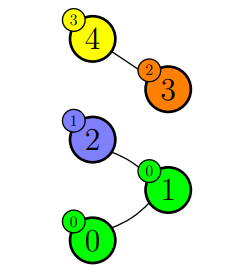
Example 1
stdin
6 6
2 0 1 1 2 1
0 2
1 3
1 5
2 4
2 5
3 5
stdout
3
Explanation
In the first sample case it is possible to start the tour in shop , go to shop , then go to shop and end the tour in shop .
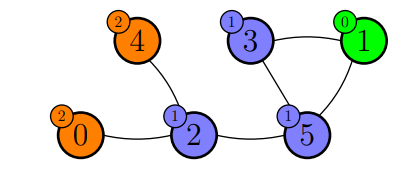
Example 2
stdin
5 3
0 0 1 2 3
0 1
2 1
3 4
stdout
-1
Explanation
In the second sample case it isn’t possible to plan a tour that passes by shops which have glass of different colors.