RoAlgo Contest #4 (avansati) | leximin

Given $N$, $M$, $K$, and a directed acyclic graph (DAG) consisting of $N$ nodes (numbered from $1$ to $N$) and $M$ edges. Find the lexicographically smallest path that ends at node $K$.

A sequence $a_1 \ a_2 \ \dots \ a_p$ is lexicographically smaller than sequence $b_1 \ b_2 \ \dots \ b_q$ if and only if:

1. $p < q$ and $a_1 = b_1$, $a_2 = b_2$, $\dots a_p = b_p$ or
2. There exists a position $pos$ such that $1 \leq pos \leq min(p, q)$ and $a_1 = b_1$, $a_2 = b_2$, $\dots$, $a_{pos-1} = b_{pos-1}$, and $a_{pos} < b_{pos}$.

Input data

The first line contains three natural numbers, $N$, $M$, and $K$, representing the number of nodes, the number of edges, and the node where the path will end. The next $M$ lines contain two numbers each, $u$ and $v$, indicating that there is an edge from node $u$ to node $v$.

Output data

The first line contains the number $L$, representing the length of the lexicographically smallest path. The second line contains a sequence of length $L$, representing the lexicographically smallest path.

Constraints and clarifications

• $1 \leq N, M \leq 500 \ 000$
• $1 \leq u, v \leq N$, $u \neq v$ for each edge

Example 1

stdin

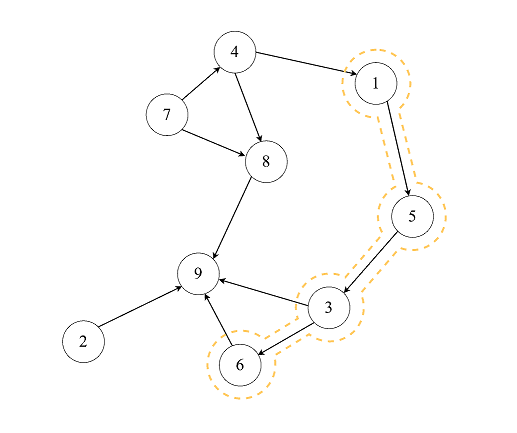
9 11 6
4 1
6 9
5 3
3 9
1 5
3 6
2 9
8 9
4 8
7 8
7 4

stdout

4
1 5 3 6