Buzdi accidentally arrived in the future, in the year 2040, during the Informatics Olympiad for the 8th grade. He managed to remember the problem statement and wants to propose this problem earlier than planned.
Task
Consider a coordinate system and points in the plane with natural number coordinates. We call a consecutive polygon a polygon formed by two consecutive points and their projections on the axis. The total area is equal to the sum of all areas of the consecutive polygons.
An Upgrade operation is defined as incrementing the coordinate of a point by 1. This operation can be:
- Used a maximum of times in total.
- Used a maximum of times for point .
Given the points, , and the vector , determine the maximum total area that can be obtained after applying up to Upgrade operations.
Input Data
The first line contains the natural numbers and separated by a space. The next lines contain two natural numbers and , separated by a space, representing the coordinates of the point on line . The last line contains natural numbers, separated by a space, representing the elements of the vector , as described in the problem statement.
Output Data
The output will contain a single real number with one decimal place, representing the maximum total area that can be obtained after applying up to Upgrade operations.
Constraints and Clarifications
- , for
- , for
- , for
- A segment is considered a polygon with an area of 0.
- For 17 points,
- For 22 points, and
Example
stdin
5 2
2 0
5 1
7 2
9 2
12 1
1 2 0 1 2
stdout
18.0
Explanation
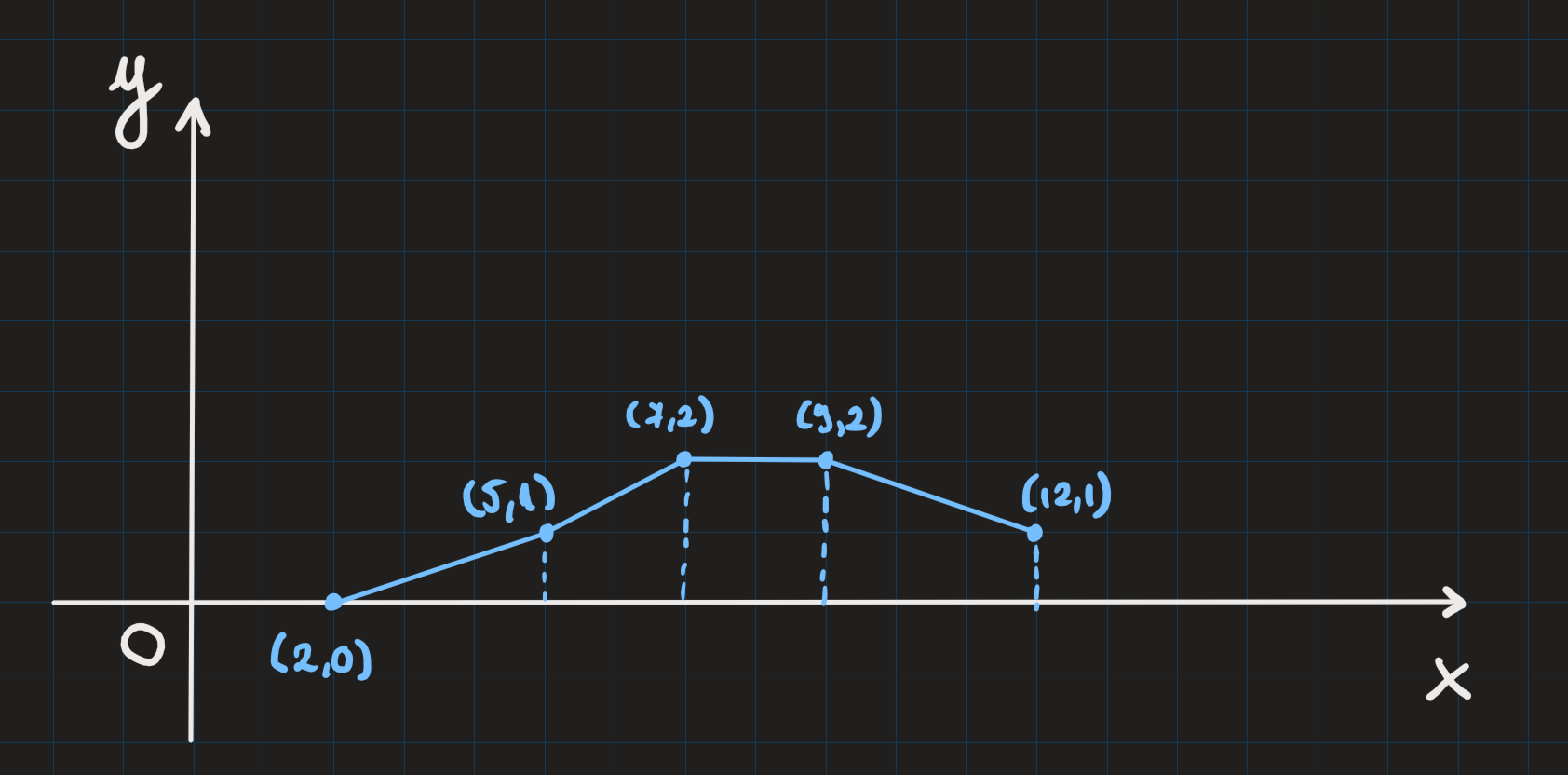
The blue points represent the points from the input data, and the dotted line represents the projection of the respective point. The first consecutive polygon is formed by the first point and the second point together with their projections on . The second consecutive polygon is formed by the second point and the third point together with their projections on and so on. We can apply the Upgrade operation to the second point and the fourth point, because and are not equal to 0. These points will now be and , and and . The total area is equal to ( represents the area of the consecutive polygon number ). This area is the maximum possible.