Se dă o mulțime de segmente. Segmentele sunt reținute prin cele două capete, iar capetele prin coordonatele lor carteziene. Un segment nu poate fi format dintr-un singur punct. Două segmente se consideră adiacente dacă ele au o extremitate comună.
Segmentele și se numesc conectate dacă există o succesiune de segmente, care începe cu și se termină cu , în care două segmente consecutive sunt adiacente.
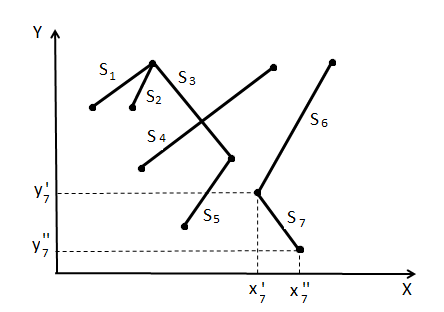
În figura alăturată, segmentele și sunt conectate, deoarece există o succesiune de segmente consecutiv adiacente, și anume , și .
O submulțime de segmente formează o rețea, dacă segmentele respective sunt conectate între ele, fără a avea conexiuni cu celelalte segmente care nu aparțin submulțimii. O mulțime de segmente poate avea una sau mai multe rețele. Pentru figura de mai sus, rețelele sunt , și .
Cerință
Cunoscând numărul de segmente și coordonatele lor, afișați numărul de rețele.
Date de intrare
Fișierul segmente.in conține pe prima linie un număr natural , reprezentând numărul de segmente. Pe fiecare din următoarele linii se găsesc coordonatele capetelor segmentului, sub forma , , , . Valorile sunt separate printr-un spațiu și sunt numere întregi.
Date de ieșire
În fişierul segmente.out fişierul segmente.out se va afişa, pe prima linie, un număr natural ce reprezintă numărul de rețele.
Restricții și precizări
Exemplu
segmente.in
7
1 7 4 8
2 6 4 8
4 8 7 4
2 4 9 7
5 2 7 4
8 3 11 8
8 3 13 1
segmente.out
3
Explicație
Exemplul din figură.