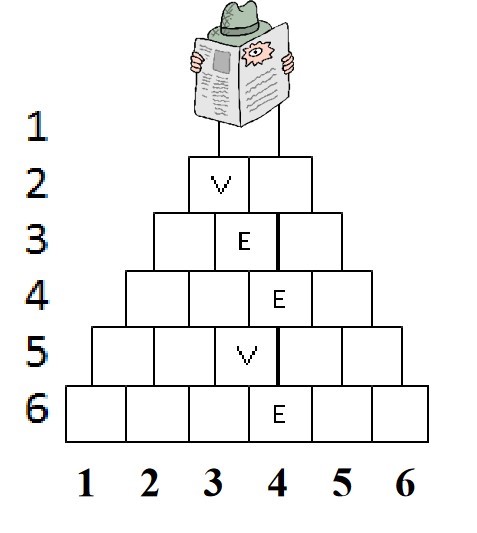
 Spionul 008 vrea să găsească o locație secretă în junglă, având asupra lui un dispozitiv de localizare. Iniţial spionul se află la intrarea în junglă pe nivelul şi cu fiecare pas, el avansează de la nivelul la nivelul , ajungând la locaţia secretă, aflată pe ultimul nivel, în poziţia faţă de marginea stângă a nivelului curent. Pentru a ajunge în locaţia secretă, el poate să se deplaseze cu o poziţie spre Sud-Est (codificat cu caracterul
Spionul 008 vrea să găsească o locație secretă în junglă, având asupra lui un dispozitiv de localizare. Iniţial spionul se află la intrarea în junglă pe nivelul şi cu fiecare pas, el avansează de la nivelul la nivelul , ajungând la locaţia secretă, aflată pe ultimul nivel, în poziţia faţă de marginea stângă a nivelului curent. Pentru a ajunge în locaţia secretă, el poate să se deplaseze cu o poziţie spre Sud-Est (codificat cu caracterul E) sau spre Sud-Vest (codificat cu caracterul V), trecând de pe nivelul pe nivelul cu viteză constantă. Numărul de poziţii de pe un nivel creşte cu faţă de nivelul anterior, conform imaginii alăturate. Numim traseu o succesiune formată din caracterele E sau V, corespunzătoare deplasării spionului de pe nivelul la locaţia secretă. Pentru exemplul din figura alăturată succesiunea de caractere VEEVE reprezintă un traseu ce corespunde locaţiei secrete din poziţia a nivelului .
Cerinţă
Cunoscând succesiunea de caractere corespunzătoare unui traseu, determinaţi:
- poziţia locației secrete de pe ultimul nivel;
- numărul de trasee distincte pe care le poate urma spionul plecând din poziţia inițială pentru a ajunge în locaţia secretă corespunzătoare traseului dat. Două trasee se consideră distincte dacă diferă prin cel puţin o poziţie.
Date de intrare
Fișierul de intrare spion.in conține pe prima linie un număr natural , iar pe a doua linie o succesiune de caractere corespunzătoare unui traseu.
Date de ieşire
Dacă valoarea lui este , atunci se va rezolva numai punctul 1 din cerință. În acest caz, fişierul de ieşire spion.out va conţine pe prima linie un număr natural ce reprezintă poziția de pe nivelul final a locației secrete. Dacă valoarea lui este , atunci se va rezolva numai punctul 2 din cerință. În acest caz, fişierul de ieşire spion.out va conţine pe prima linie un număr natural ce reprezintă numărul de trasee distincte modulo .
Restricţii şi precizări
- lungimea şirului paşilor ;
- pentru din teste, ;
- pentru alte din teste, şi lungimea secvenţei de caractere ;
- pentru alte din teste, şi lungimea secvenţei de caractere ;
- pentru alte din teste, şi lungimea secvenţei de caractere .
Exemplul 1
spion.in
1
VEEVE
spion.out
4
Explicație
Locația secretă este în poziţia de pe nivelul .
Exemplul 2
spion.in
2
VEV
spion.out
3
Explicație
Există trei trasee: VVE, VEV, EVV.
Exemplul 3
spion.in
2
EVEVVEVEEE
spion.out
210