joc

Costel are o mare pasiune pentru rezolvarea cubului Rubik, atât de mare încât a început să facă cercetări și calcule diverse pornind de la acest joc. Ultima lui idee, inspirată de cubul Rubik, folosește un cub de latură $2$ unități, compus din $8$ cuburi cu latura de o unitate (cub unitate), având fețele exterioare colorate. Fiecare cub unitate are $3$ fețe exterioare şi fiecare dintre acestea este colorată cu una din cele $10$ culori disponibile, codificate prin cifrele de la $0$ la $9$.

Figura 1	Figura 2

Identificarea cuburilor unitate se face conform specificaţiilor din Figura 1. Cubul care nu este vizibil în Figura 1 are coordonatele $(1, 1, 2)$. Cubul lui Costel permite efectuarea următoarelor tipuri de mutări, asemănătoare cu cele din cubul Rubik:

• M1: Paralelipipedul $1$ conține cuburile unitate de coordonate: $(1, 1, 1); (1, 2, 1); (2, 1, 1); (2, 2, 1)$. Acesta este un disc așezat orizontal și poate fi rotit cu $90$ de grade către dreapta, în sensul acelor de ceasornic.
• M2: Paralelipipedul $2$ conține cuburile unitate de coordonate: $(1, 1, 2); (1, 2, 2); (2, 1, 2); (2, 2, 2)$. Acesta este un disc așezat orizontal și poate fi rotit cu $90$ de grade către dreapta, în sens invers acelor de ceasornic.
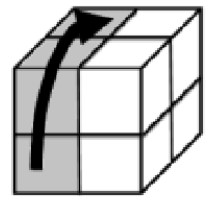
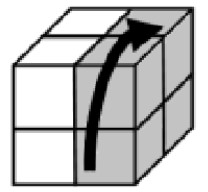
• M3: Paralelipipedul $3$ conține cuburile unitate de coordonate: $(1, 1, 1); (2, 1, 1); (1, 1, 2); (2, 1, 2)$. Acesta este un disc așezat vertical și poate fi rotit cu $90$ de grade către planul îndepărtat, în sens invers acelor de ceasornic.
• M4: Paralelipipedul $4$ conține cuburile unitate de coordonate: $(1, 2, 1); (2, 2, 1); (1, 2, 2); (2, 2, 2)$. Acesta este un disc așezat vertical și poate fi rotit cu $90$ de grade către planul îndepărtat, în sensul acelor de ceasornic.

M1	M2	M3	M4

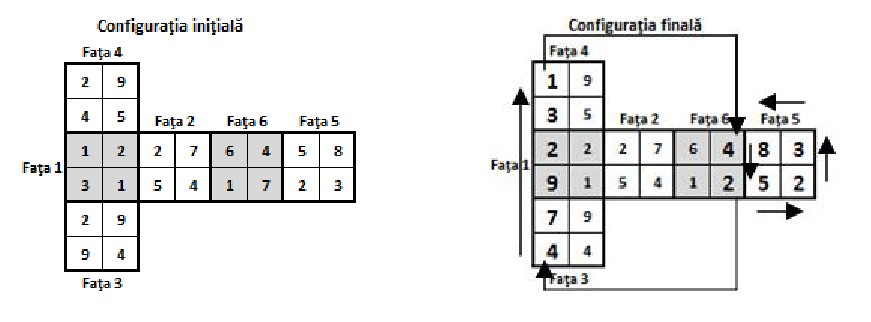
Prin configurație se înțelege memorarea culorii fiecărei fețe exterioare a celor $8$ cuburi unitate, deci culorile celor $24$ de feţe exterioare. Aplicând o succesiune validă de mutări se obține o altă configurație. Pentru ușurința memorării unei configurații, Costel utilizează desfășurarea în plan a celor $6$ fețe ale cubului său după modelul din Figura 2, care ilustrează modul în care sunt dispuse fețele în desfăşurare. Fiecare faţă a cubului conţine patru feţe exterioare ale cuburilor unitate având, în ordine, coordonatele specificate în figură.

Cerință

Fiind date o configuraţie iniţială şi o configuraţie finală ale jocului, determinați numărul minim de mutări prin care se poate ajunge de la configurația initială la configurația finală şi succesiunea corespunzătoare de mutări prin care se poate obţine configuraţia finală.

Date de intrare

Fişierul de intrare joc.in conţine:

• $12$ linii corespunzătoare configuraţiei iniţiale - câte două linii pentru fiecare din cele şase feţe; pe fiecare linie sunt memorate câte două cifre, separate prin exact un spaţiu (pe primele două linii se află elementele feței $1$, pe următoarele două linii se află elementele feței $2$, ..., pe liniile $11$ și $12$ se află elementele feței $6)$.
• Pe următoarele $12$ linii se află elementele configurației finale - câte două linii pentru fiecare din cele şase feţe; pe fiecare lnie sunt memorate câte două cifre, separate prin exact un spaţiu.

Date de ieșire

Fişierul de ieşire joc.out va conţine:

• Pe prima linie, un număr natural $MIN$, reprezentând numărul minim de mutări determinat.
• Pe următoarele $MIN$ linii succesiunea de mutări care transformă configuraţia iniţială în cea finală, pe fiecare linie fiind scris un număr natural cuprins între $1$ și $4$ ce reprezintă numărul asociat unei mutări.

Restricții și precizări

• Se garantează că pentru toate datele de test există soluție, aceasta având cel mult $11$ mutări.
• Orice soluţie cu număr minim de mutări care conduce la obţinerea configuraţiei finale va obţine punctajul maxim.

Exemplu

joc.in

1 2
3 1
2 7
5 4
2 9
9 4
2 9
4 5
5 8
2 3
6 4
1 7
2 2
9 1
2 7
5 4
7 9
4 4
1 9
3 5
8 3
5 2
6 4
1 2

joc.out

1
3

Explicație

Se efectuează mutarea discului $3$, către planul îndepărtat, adică mutarea $3$.