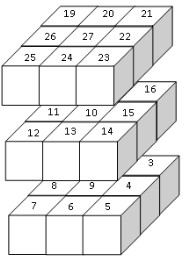
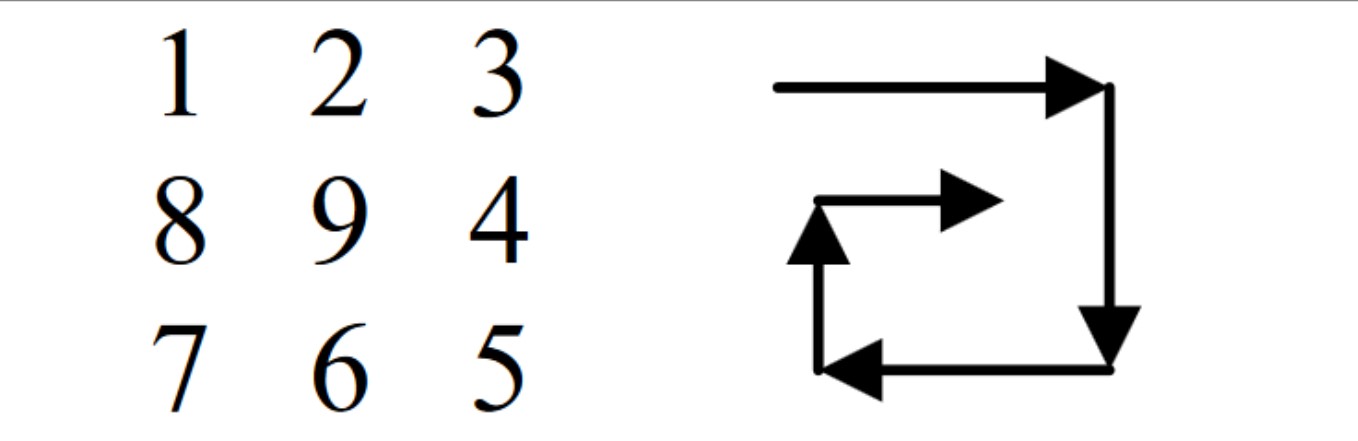
 Sărbătorile de iarnă tocmai s-au încheiat. Florinel dorește să-și ajute părinții la despodobirea bradului. Tubul luminos pe care l-au folosit anul acesta este mai special. Are becuri luminoase numerotate de la 1 la , iar fiecare bec care este inscripționat cu un număr prim, va rămâne mereu aprins. Cutia în care trebuie strâns tubul este un cub de latură N. Becul cu numărul 1, trebuie pus în colțul de coordonate , restul în spirală până la umplerea nivelului, apoi nivelul următor în sens invers, ș.a.m.d.
Sărbătorile de iarnă tocmai s-au încheiat. Florinel dorește să-și ajute părinții la despodobirea bradului. Tubul luminos pe care l-au folosit anul acesta este mai special. Are becuri luminoase numerotate de la 1 la , iar fiecare bec care este inscripționat cu un număr prim, va rămâne mereu aprins. Cutia în care trebuie strâns tubul este un cub de latură N. Becul cu numărul 1, trebuie pus în colțul de coordonate , restul în spirală până la umplerea nivelului, apoi nivelul următor în sens invers, ș.a.m.d.
| Nivel 1 | Nivel 2 | Nivel 3 |
|---|---|---|
 |
 |
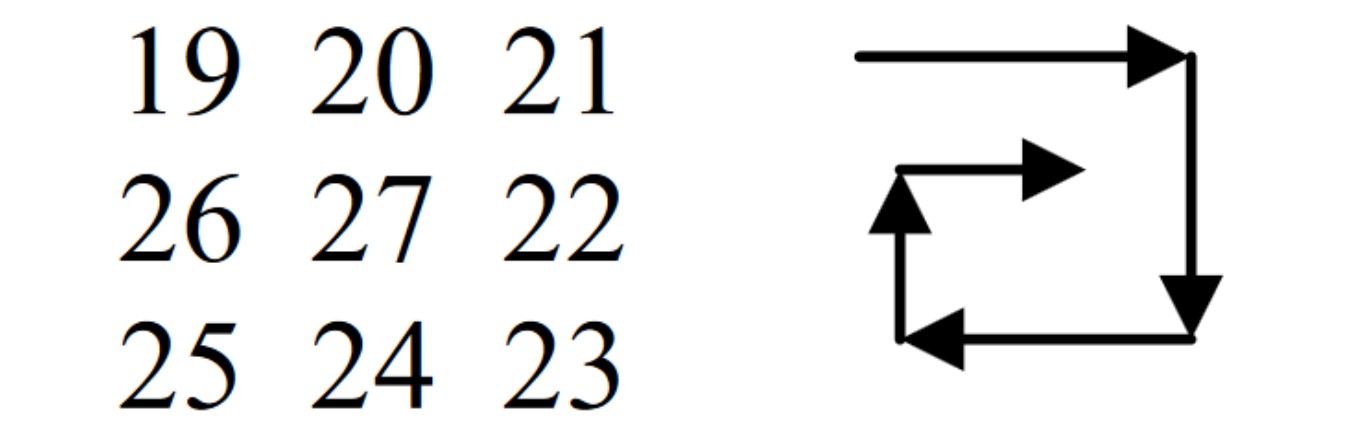 |
| Fața 1 (spate) | Fața 2 (dreapta) | Fața 3 (frontal) | Fața 4 (stânga) |
|---|---|---|---|
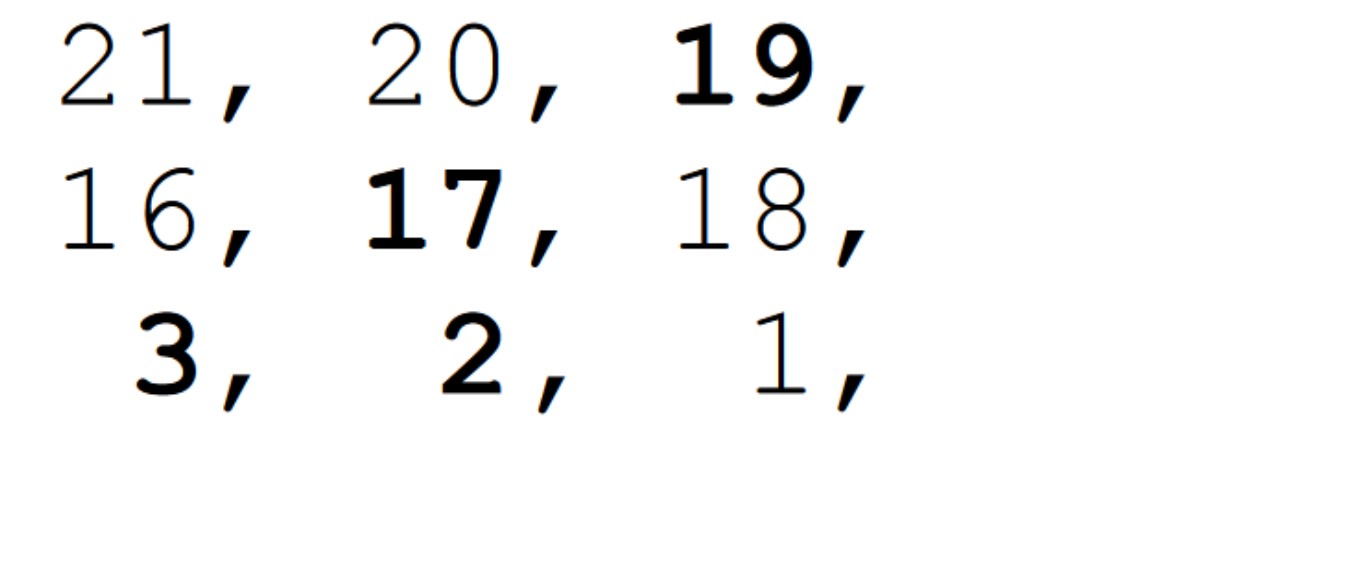 |
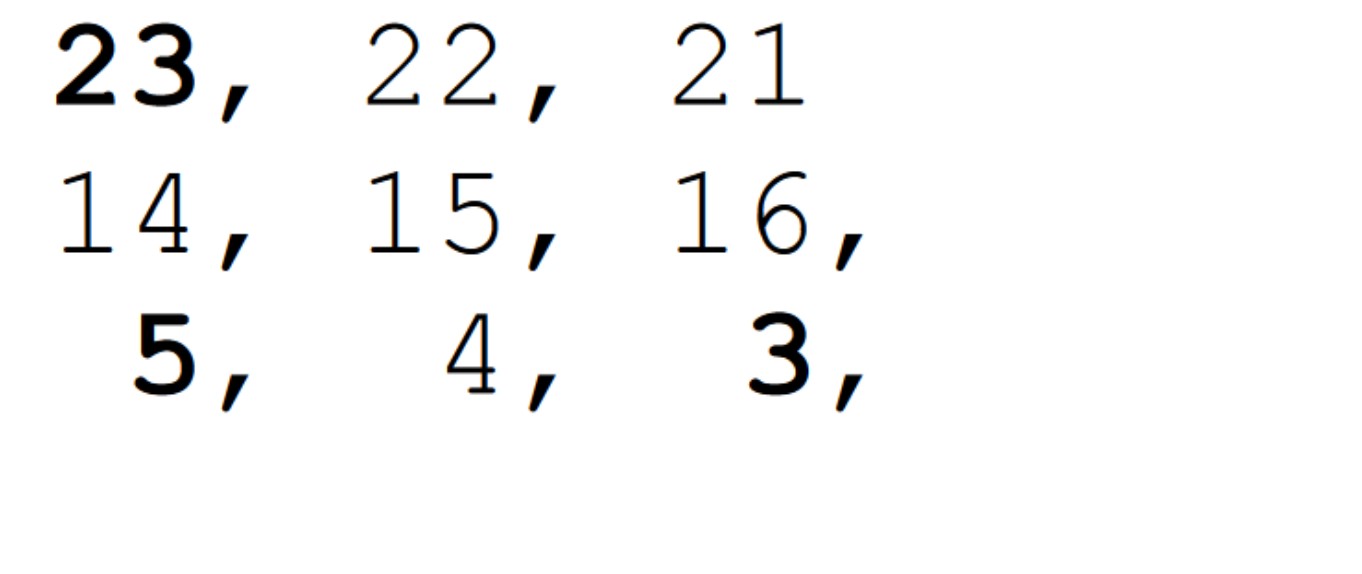 |
 |
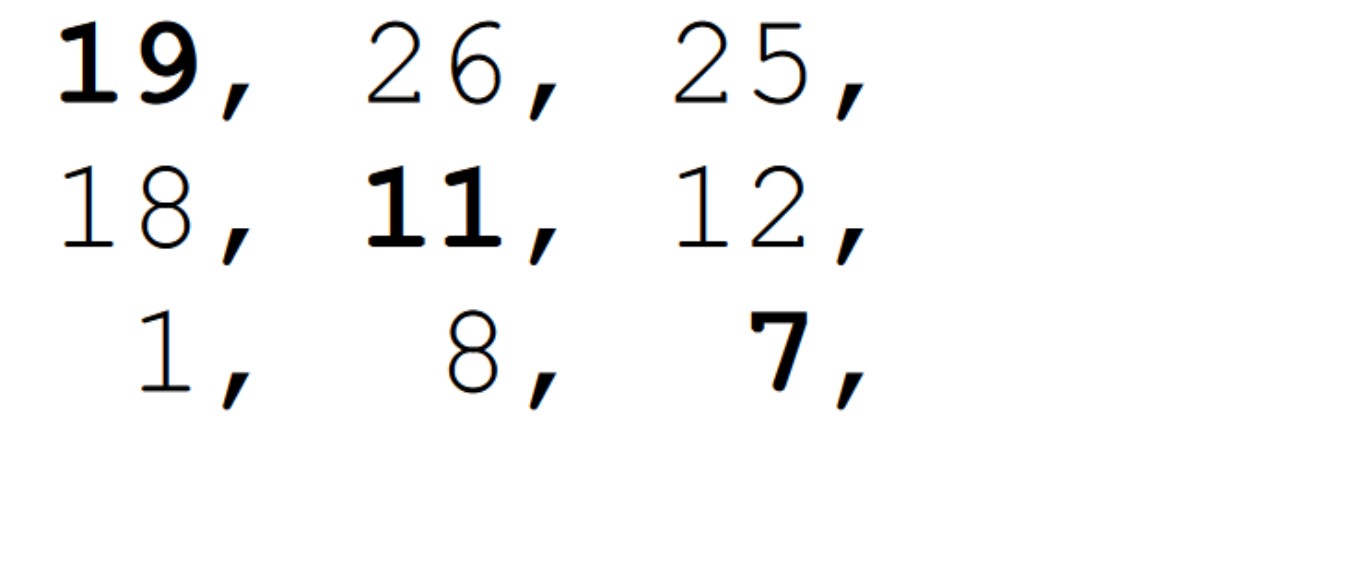 |
Cerinţă
Cunoscând latura N a cubului, să se umple cubul cu tubul luminos (becurile fiind legate crescător), apoi să se determine:
- Coordonatele ale becului cu numărul . ( - linia, - coloana, - înălțimea);
- Numărul de becuri luminoase situate pe fiecare față a cubului.
Date de intrare
Fişierul de intrare cub.in conţine pe prima linie un număr natural . Pentru toate testele de intrare, numărul poate avea doar valoarea sau valoarea . Pe a doua linie a fișierului de intrare, sunt scrise două numere naturale și separate printr-un spațiu reprezentând dimensiunea cubului și valoarea becului pentru care trebuie determinate coordonatele.
Date de ieșire
- Dacă valoarea lui este , se va rezolva numai cerinţa . În acest caz, în fişierul de ieşire
cub.outse vor scrie trei numere naturale , separate prin câte un spațiu, reprezentând coordonatele becului cu valoarea . - Dacă valoarea lui este , se va rezolva numai cerinţa . În acest caz, fişierul de ieşire
cub.outva conține linii. Pe fiecare linie , se va scrie câte un număr natural , reprezentând numărul de becuri inscripționate cu numere prime de pe fața .
Restricții și precizări
- ;
- ;
- Pentru rezolvarea corectă a primei cerinţe se acordă 20 de puncte, iar pentru cerința a doua se acordă 80 de puncte.
- Pentru dintre teste: ;
- Pentru dintre teste: ;
- Pentru dintre teste: .
Exemplul 1
cub.in
1
3 10
cub.out
2 2 2
Explicație
Atenție! Pentru acest test se rezolvă doar cerința 1. Linia , coloana , nivel – este becul .
Exemplul 2
cub.in
2
3 10
cub.out
4
3
4
3
Explicație
Atenție! Pentru acest test se rezolvă doar cerința 2.
- – becuri inscripționate cu numere prime pe fața : , , ,
- – becuri inscripționate cu numere prime pe fața : , ,
- – becuri inscripționate cu numere prime pe fața : , , ,
- – becuri inscripționate cu numere prime pe fața : , ,