geogra

Pasionați de geografie, Alex și Răzvan joacă online Geoguessr. Harta lumii este alcătuită din $N$ locații numerotate de la $1$ la $N$, fiecare desemnând un punct în plan de coordonate ($X_i$, $Y_i$). Alex a studiat atent toate cele $N$ locații și a determinat o listă de $L$ caracteristici de interes pentru locațiile date, numerotate de la $1$ la $L$. De exemplu, caracteristica $1$ ar putea fi “se află respectiva locație în Europa?”, iar caracteristica $2$ ar putea fi “se vorbește limba spaniolă în locația respectivă?”, și așa mai departe. Pentru fiecare locație $i$ și fiecare caracteristică $j$ se consideră cunoscută valoarea $Z_{i,j}$ ∈ {$0$, $1$} cu proprietatea că $Z_{i,j}$ = $1$ dacă și numai dacă locația $i$ are caracteristica $j$. De exemplu, dacă locația $1$ se află în Asia și acolo se vorbește limba spaniolă, atunci am avea $Z_{1, 1} = 0$ și $Z_{1, 2} = 1$.

Un joc de Geoguessr este format din $Q$ runde. La o rundă, calculatorul alege o locație $i$ din cele $N$, fără a o dezvălui lui Alex. În schimb, Alex primește câteva ilustrații cu locul respectiv, scopul lui Alex fiind acela de a descoperi locația $i$. Analizând atent doar ilustrațiile, Alex poate determina pentru orice caracteristică $j$ dacă locația $i$ o are sau nu. Totuși, timpul pentru fiecare rundă fiind limitat, Alex nu va reuși mereu să afle în timp util valorile $Z_{i, j}$ pentru toate caracteristicile $j$, ci doar pentru unele. Așadar, dorind să fie cât mai eficient, Alex și-a format următoarea strategie de joc, moștenită de la Bunicul lui: prima dată Alex va afla valoarea $Z_{i,T_1}$, apoi, dacă a mai rămas timp, Alex va afla valoarea $Z_{i,T_2}$, apoi valoarea $Z_{i,T_3}$, și așa mai departe până când expiră timpul alocat rundei. În funcție de limita de timp a rundei (care poate varia de la o rundă la alta), cu această strategie este posibil ca Alex să afle mai multe sau mai puține informații despre locație, inclusiv niciuna (adică nicio valoare $Z_{i, j}$ descoperită). Vom nota cu $R_1$, $R_2$, …,$R_L$ informațiile descoperite de Alex până la finalul rundei. Mai exact, $R_j = Z_{i,j}$ dacă Alex a apucat să afle dacă locația $i$ are caracteristica $j$ în timp util, sau $R_j = -1$ altfel.

Atenție! Strategia lui Alex, reprezentată de șirul $T_1$, $T_2$, …, $T_L$, este aceeași pentru toate cele $Q$ runde. Șirul $T_1$, $T_2$, …, $T_L$ este format din valori distincte și $T_1$, $T_2$, ..., $T_L$ ∈ {$1$, $2$, ..., $L$}.

Cerință

La finalul unei runde este posibil ca mai multe locații din cele $N$ să corespundă cu șirul $R$ de informații aflate de Alex, așa că acesta își pune două întrebări existențiale:

Care este numărul $K$ de locații dintre cele $N$ care respectă șirul $R$ de informații aflate pe parcursul rundei? Spunem că o locație $i$ respectă șirul $R$ dacă pentru orice caracteristică $j$ avem ca $R_j$ = $Z_{i, j}$ sau $R_j = -1$.
Se dă câte o valoare $W_i$ pentru fiecare locație $i$ din cele $N$, $1 \leq i \leq N$. Considerând locațiile care respectă șirul $R$, fie acestea $1 \leq i_1, i_2, ..., i_K \leq N$, pentru un punct $P$ de coordonate întregi ($A$, $B$) din plan, nu neapărat unul corespunzător unei locații dintre cele $N$, definim
$d_P$ = $W_{i_1}(|A−X_{i_1}|+|B−Y_{i_1}|) + W_{i_2}(|A−X_{i_2}|+|B−Y_{i_2}|) +. . .+ W_{i_K}(|A−X_{i_K}|+|B−Y_{i_K}|)$
Care este punctul $P$ din plan pentru care $d_P$ este minim? Dacă sunt mai multe astfel de puncte $P$, se cere cel cu $A$ minim. Dacă încă este egalitate, atunci se cere cel cu $B$ minim.
Se dă un număr $C$ ∈ {$1$, $2$}. Pentru $C = 1$ să se afișeze răspunsul la prima întrebare a lui Alex pentru fiecare din cele $Q$ runde. Pentru $C = 2$ să se afișeze răspunsul la a doua întrebare a lui Alex pentru fiecare din cele $Q$ runde.

Date de intrare

Pe prima linie a fișierului geogra.in se află numărul natural $C$, reprezentând cerința care trebuie rezolvată. Pe cea de-a doua linie se află numerele naturale $N$ și $L$, reprezentând numărul locațiilor și, respectiv, numărul caracteristicilor studiate de Alex. Urmează descrierile celor $N$ locații, în ordine de la $1$ la $N$, fiecare pe câte doua linii. Descrierea unei locații $i$ se face după cum urmează:

Pe prima linie se afla numerele naturale $X_i$ și $Y_i$. Dacă $C = 2$, în continuarea acestor doua valori se află numărul natural $W_i$. Valorile de pe linie sunt separate prin spații.
Pe a doua linie se află $Z_{i,1}$, $Z_{i,2}$, ..., $Z_{i,L}$, separate prin spații.
Pe următoarea linie se află numărul natural $Q$, reprezentând numărul de runde din cadrul jocului. Urmează descrierile celor $Q$ runde, în ordine de la $1$ la $Q$, fiecare pe câte o linie. Descrierea unei runde $i$ se face prin șirul de valori $R_1$, $R_2$, …, $R_L$ găsit de Alex în runda respectivă, valorile fiind separate prin spații.

Date de ieșire

Fișierul de ieșire geogra.out va conține $Q$ linii. Dacă $C = 1$, linia $i$ va conține numărul locațiilor care respectă șirul $R$ de informații aflate de Alex în runda $i$. Dacă $C = 2$, linia $i$ va conține doua numere naturale $A$ și $B$, reprezentând coordonatele punctului $P$ căutat pentru care $d_P$ este minim în runda $i$, unde $1 \leq i \leq N$.

Restricții și precizări

• $1 \leq N, Q \leq 100 \ 000$;
• $1 \leq L \leq 30$;
• $1 \leq X_i, Y_i \leq 1 \ 000 \ 000 \ 000$, oricare ar fi $1 \leq i \leq N$;
• $1 \leq W_i \leq 10 \ 000$, oricare ar fi $1 \leq i \leq N$;
• $Z_{i, j}$ ∈ {$0$, $1$}, oricare ar fi $1 \leq i \leq N$, $1 \leq j \leq L$;
• $R_j$ ∈ {$-1$, $0$, $1$}, oricare ar fi $1 \leq j \leq L$;
• $1 \leq K \leq N$, pentru fiecare rundă din cele $Q$;
• Nu există două locații care desemnează același punct din plan;
• Se garantează că Alex respectă aceeași strategie, reprezentată de șirul $T_1$, $T_2$, …, $T_N$, în fiecare din cele $Q$ runde.

Exemplul 1

geogra.in

1
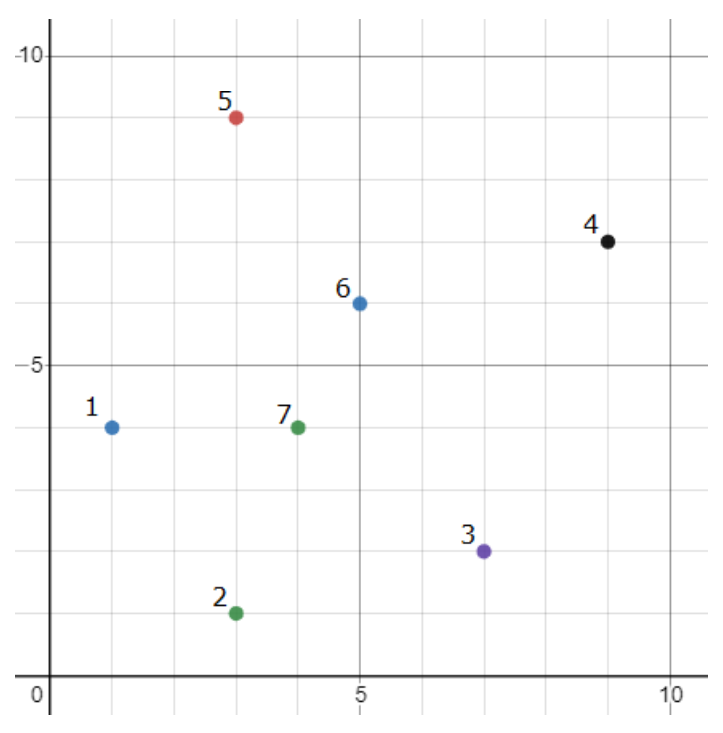
7 4
1 4
1 1 0 1
3 1
1 1 1 0
7 2
0 1 0 0
9 7
1 0 1 0
3 9
0 0 0 0
5 6
0 0 1 0
4 4
1 1 0 0
5
1 0 1 0
-1 0 -1 0
-1 -1 -1 -1
-1 1 -1 -1
1 1 -1 0

geogra.out

1
3
7
4
2

Exemplul 2

geogra.in

2
7 4
1 4 1
1 1 0 1
3 1 1
1 1 1 0
7 2 5
0 1 0 0
9 7 1
1 0 1 0
3 9 2
0 0 0 0
5 6 1
0 0 1 0
4 4 1
1 1 0 0
5
1 0 1 0
-1 0 -1 0
-1 -1 -1 -1
-1 1 -1 -1
1 1 -1 0

geogra.out

9 7
3 7
5 2
7 2
3 1

Explicații

În cazul acestor exemple, strategia lui Alex este $T_1 = 2$, $T_2 = 4$, $T_3 = 1$, $T_4 = 3$.

Spre exemplu, în runda $2$ Alex află mai întâi valoarea $R_2$, apoi valoarea $R_4$, dar, din cauza faptului că rămâne fără timp, nu mai reușește sa afle nici valoarea $R_1$ și nici valoarea $R_3$.

Pentru runda $1$, locația care respectă șirul $R$ găsit de Alex este $4$. Pentru $C = 2$, punctul cerut este $P(9,7)$, iar $d_P = 0$.

Pentru runda $2$, locațiile care respectă șirul $R$ găsit de Alex sunt $4, 5, 6$. Pentru $C = 2$, punctul cerut este $P(3,7)$, iar $d_P = 13$.

Pentru runda $3$, locațiile care respectă șirul $R$ găsit de Alex sunt $1, 2, 3, 4, 5, 6, 7$. Pentru $C = 2$, punctul cerut este $P(5,2)$, iar $d_P = 53$.

Pentru runda $4$, locațiile care respectă șirul $R$ găsit de Alex sunt $1, 2, 3, 7$. Pentru $C = 2$, punctul cerut este $P(7,2)$, iar $d_P = 18$.

Pentru runda $5$, locațiile care respectă șirul $R$ găsit de Alex sunt $2, 7$. Pentru $C = 2$, punctul cerut este $P(3,1)$, iar $d_P = 4$.