Un polyomino este o figură geometrică plană compactă formată din una sau mai multe piese de domino, pătrate egale de latură . Două piese se consideră alăturate dacă au o latură comună.
Exemple de Polyominouri cu piese:

Două Polyominouri se consideră identice dacă sunt formate din acelaşi număr de piese şi au aceeaşi configuraţie sau configuraţia unuia se poate obţine prin oglindirea celuilalt. În caz contrar cele două Polyominouri se consideră distincte.
| Polyominouri distincte | 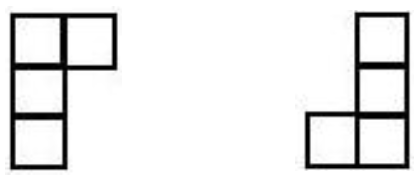 |
Polyominouri care nu sunt distincte | 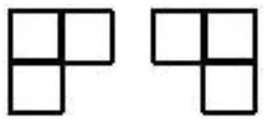 |
|---|
Un polyomino poate fi rotit cu , şi , în sens trigonometric. Prin rotaţie se obţin alte Polyominouri, nu neapărat identice cu cel inţial.
Exemplu:
| Prin rotaţia polyomino-ului |  |
se obţin: |  |
|---|
Niciunul dintre aceste Polyominouri nu este identic cu cel iniţial.
Un polyomino este convex dacă prin parcurgerea succesivă a linilor sau coloanelor nu se întâlnesc găuri.
| Polyomino convex |  |
Polyominouri neconvexe |  |
|---|
Un polyomino este oblic convex (skew polyomino) dacă este convex şi prin parcurgerea succesivă a coloanelor de la stânga la dreapta acestea nu descresc în înălţime. Altfel spus, partea de jos a coloanei din stânga este întotdeauna mai mică sau egală ca înălţime cu partea de jos a coloanei din dreapta. În mod similar, partea de sus a coloanei din stânga este întotdeauna mai mică sau egală cu partea de sus a coloanei din dreapta.
Exemple:
| Polyominouri oblice |  |
Polyominouri care nu sunt oblice | 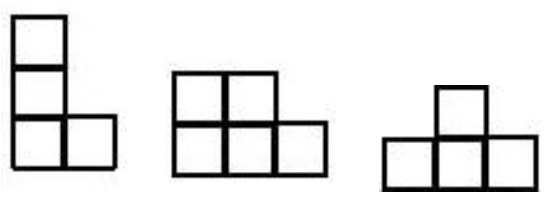 |
|---|
Cerință
Să se determine numărul de Polyominouri oblice distincte care au perimetrul egal cu . Acest număr poate să fie mare, de aceea ne interesează rezultatul modulo .
Date de intrare
Fişierul de intrare poly.in conţine pe prima linie un număr natural .
Date de ieșire
Fişierul de ieşire poly.out conţine pe prima linie un număr natural ce reprezintă numărul de Polyominouri oblice care au perimetrul egal cu , număr afişat modulo .
Restricții și precizări
Exemplu
poly.in
3
poly.out
5
Explicație
Sunt Polyominouri care respectă cerinţa:
