intersectii

Dreptunghiul $ABCD$ are laturile de lungimi $w$ şi $h$, numere naturale pare.

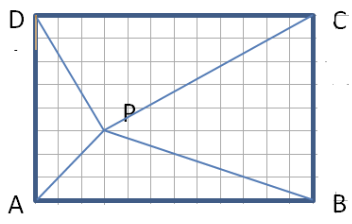
Acest dreptunghi este desenat pe o foaie de matematică şi este descompus în $w \cdot h$ pătrate de latură $1$. Vârfurile $A$, $B$, $C$ şi $D$ sunt plasate în colţurile unor pătrate de latură $1$. Se alege un punct $P$ din interiorul dreptunghiului $ABCD$, situat în colţul unui pătrat de latură $1$ şi se uneşte prin segmente de dreaptă cu cele patru colţuri ale dreptunghiului. Unele segmente intersectează pătrate de latură $1$ în exact două puncte distincte, altele într-un singur punct.

Numim pătrat $2$-intersectat, un pătrat de latură $1$ intersectat de un segment în exact $2$ puncte distincte. În dreptunghiul din figura alăturată, segmentul $PA$ trece prin $3$ pătrate $2$-intersectate, segmentul $PB$ trece prin $9$ pătrate $2$-intersectate, segmentul $PC$ trece prin $13$ pătrate $2$-intersectate, iar segmentul $PD$ prin $7$.

Cerință

Se dau două numere naturale $w$ şi $h$ reprezentând lungimile laturilor dreptunghiului $ABCD$, un număr natural $n$ şi $n$ numere naturale $x_1, x_2, \ldots x_n$. Punctul $P$ se plasează, pe rând, în toate punctele interioare dreptunghiului $ABCD$ care sunt colţuri ale unor pătrate de latură $1$. Pentru fiecare valoare $x_i$ ( $1 \leq i \leq n$ ), determinaţi numărul de segmente distincte care trec prin exact $x_i$ pătrate $2$-intersectate.

Date de intrare

Fişierul de intrare intersectii.in conţine pe prima linie trei numere naturale $w$, $h$ (reprezentând dimensiunile dreptunghiului) şi $n$. Următoarele $n$ linii conţin câte un număr natural $x_i$ cu semnificaţia de mai sus.

Date de ieșire

Fişierul de ieşire intersectii.out va conţine $n$ linii. Pe fiecare linie $i$ va fi scris numărul de segmente care trec prin exact $x_i$ pătrate $2$-intersectate, obţinute după plasarea punctului $P$ în fiecare colţ al unui pătrat de latură $1$ din interiorul dreptunghiului $ABCD$.

Restricții și precizări

• $2 \leq w, h \leq 2 \ 000$ numere naturale pare
• $2 \leq n \leq 100 \ 000$
• Punctul $P$ se alege doar în interiorul dreptunghiului
• pentru $40$% din teste $2 \leq w, n, h \leq 500$

Exemplu

intersectii.in

4 6 2
3
5

intersectii.out

12
4

Explicație

Se pot obţine $12$ segmente care trec prin exact $3$ pătrate $2$-intersectate şi $4$ segmente care trec prin exact $3$ pătrate $2$-intersectate.