Tânărul ninja Enaz se pregăteşte de marea finală de aruncări cu shurikene. În funcție de distanța la care ajung shurikenele în urma aruncărilor concurenții primesc puncte. Zona de punctare este definită de subzone consecutive, adiacente, fiecare având lungimi și punctaje diferite. Astfel, dacă un concurent aruncă un shuriken la o distanță acoperită de o subzonă de punctaj , el va primi puncte, însă dacă distanța nu este acoperită de nicio subzonă, punctajul lui va rămâne neschimbat. Dacă shurikenul se află la granița unei subzone, se consideră că el aparține acelei subzone. Dacă însă un shuriken se află la granița a subzone, se consideră că el aparține subzonei la distanță mai mare de origine. Cu câteva ore înaintea startului, Maestrul Uw are o viziune. Acesta știe cu exactitate la ce distanță de origine vor ajunge cele shurikene aruncate de Enaz. Având aceste informații el își pune întrebarea: Unde ar trebui să înceapă zona de punctare pentru ca Enaz să obțină cel mai mare punctaj posibil și care este acest punctaj?
Cerință
Să se afișeze distanța de la origine la începutul zonei de punctare ce aduce cele mai multe puncte lui Enaz și acest număr maxim de puncte. În cazul în care există mai multe astfel de distanțe, se afișează cea mai mică.
Date de intrare
Pe prima linie se găsește numărul de ordine al grupului de teste din care face parte testul.
Pe a doua linie se găsesc două numere naturale, și .
Pe a treia linie se găsesc numere naturale, unde , reprezentând distanțele de la origine la care au ajuns shurikenele aruncate de Enaz.
Pe următoarele linii se găsesc câte două numere, unul natural și anume și unul întreg și anume unde , reprezentând distanța respectiv punctajul fiecărei subzone în ordine de la cea mai apropiată de origine la cea mai depărtată.
Date de ieșire
Pe prima linie se vor găsi două numere, unul natural și unul întreg reprezentând distanța respectiv punctajul cerute în cerință.
Restricții și precizări
- Distanța de la origine la începutul zonei de punctare , cu alte cuvinte zona de punctare nu poate începe înaintea originii.
- Grupurile de teste sunt următoarele:
| # | Punctaj | Restricții |
|---|---|---|
| 0 | 0 | Exemplu |
| 1 | 7 | |
| 2 | 11 | |
| 3 | 13 | |
| 4 | 39 | |
| 5 | 30 | Fără restricții suplimentare |
Exemplu
stdin
0
6 4
8 11 12 5 9 4
2 4
1 -5
3 2
1 3
stdout
4 15
Explicație
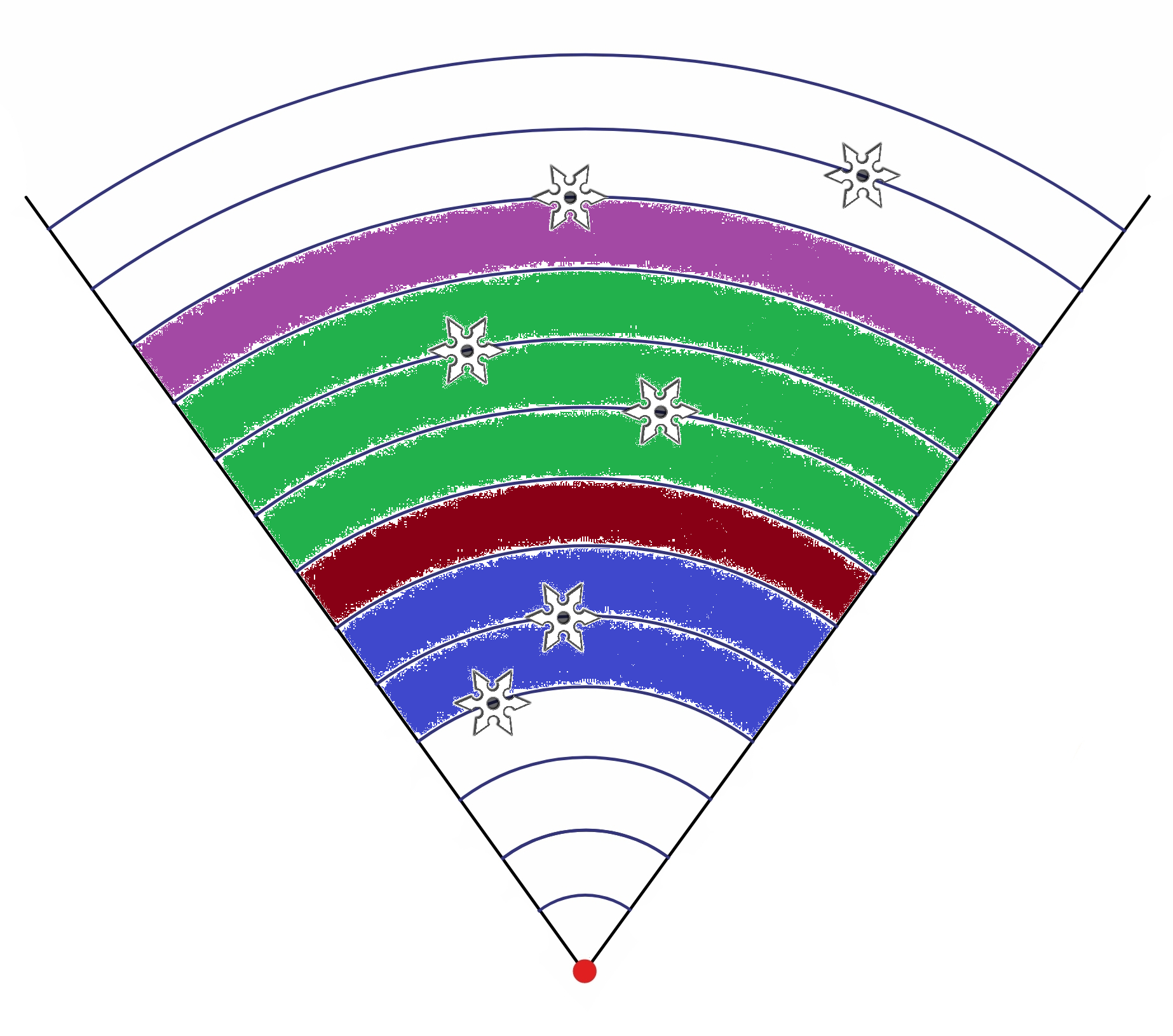
După cum se poate vedea în imagine, dacă zona de punctare începe de la distanța , atunci shurikenele de la distanțele și vor aduce fiecare câte puncte, shurikenele de la distanțele și vor aduce fiecare câte puncte, shurikenul de la distanța va aduce puncte, iar cel de la distanța nu va aduce niciun punct fiind în afara zonei de punctare. Punctajul total este 15, acesta fiind maximal.