Task
Little Polygon received a gift from his wonderful friend Little Circle. In the gift there was a drawing of an vertex polygon, each vertex being labeled with an integer from to , and a triangulation of it, e.g:
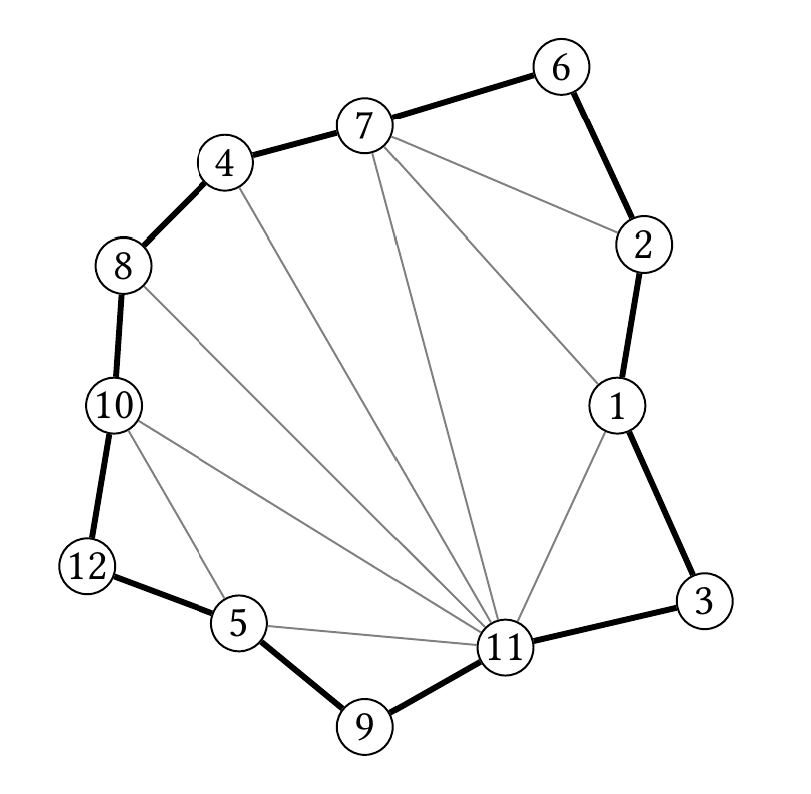
There was also a note, which asked Little Polygon to write every number from to once, one number inside each triangle, so that number is written in a triangle that has vertex as a corner. For example:
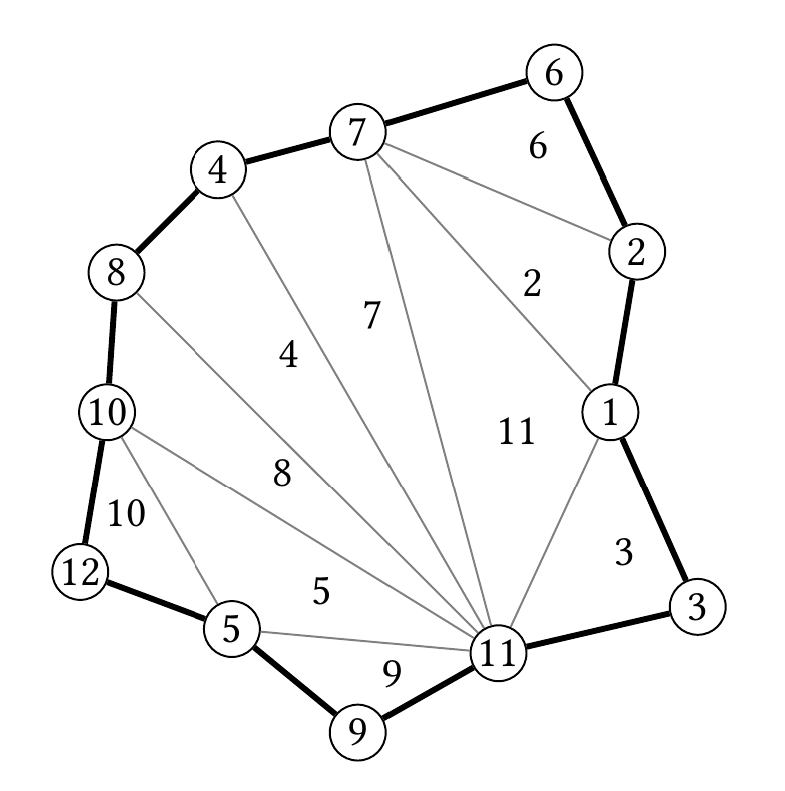
Note that every number from to has been written exactly once. Furthermore, each number is in a triangle which has as a vertex:
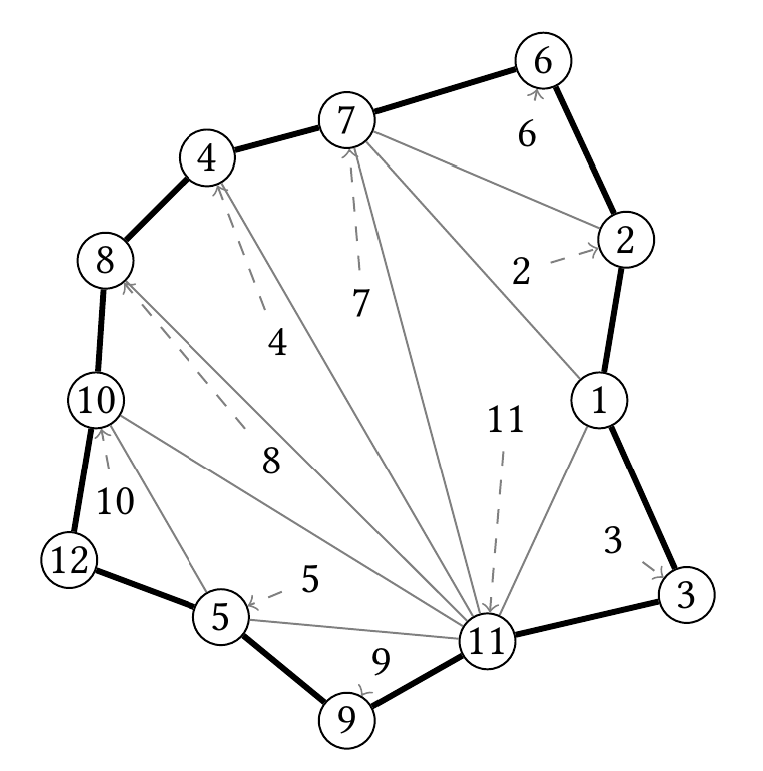
Help Little Polygon find a way of writing these numbers inside the triangles, as well as counting how many ways of doing this there are.
Input data
Each input file will contain multiple test cases.
The first line of the input contains , the number of test cases.
Each test case begins with a line containing , the number of sides of the input polygon. The second line contains labels of the vertices of the polygon, in counter-clockwise order. The next lines each contain a triple, representing the vertices of a triangle in the triangulation.
Output data
Output two lines for each test case. On the first line, output a valid way of writing numbers in the triangles (output the numbers in the same order as the triangles in the input file). On the second line, output how many ways there are of doing this, modulo .
Constraints and clarifications
- If only the first line of the output for every test case in an output file is correct, you will receive of the score for that file. If only the second line of the output for every test case in an output file is correct, you will also receive of the score for that file. If the entire file is correct, you will receive of the score for that file.
- Note! Output two lines for each test case, the first containing integers, the second containing one integer, all of which can be represented as
int-type variables, even if one of the lines is wrong. Otherwise you will receive the evaluation judgmentInvalid output format. - .
- .
- The sum of over all test cases in one file is at most
- The triangles given in any test case form a valid triangulation.
| # | Points | Constraints |
|---|---|---|
| 1 | 8 | and |
| 2 | 11 | and |
| 3 | 23 | and |
| 4 | 17 | and are neighbors in the polygon |
| 5 | 14 | every triangle includes vertex |
| 6 | 9 | every triangle includes vertex |
| 7 | 18 | No further restrictions |
Example
stdin
1
12
1 2 6 7 4 8 10 12 5 9 11 3
11 5 9
1 7 11
10 5 12
1 2 7
6 7 2
3 11 1
11 10 8
11 10 5
4 8 11
7 4 11
stdout
9 11 10 2 6 3 8 5 4 7
9
Explanation
This is the example drawn above in the statement.