Antonia recently visited London. There, she was impressed by the large number of subway stations, which, to her surprise, formed a tree. While getting bored on the subway, Antonia wondered if she could generate a tree with the minimum number of nodes that would have exactly paths from to , for any nodes , , provided that is an ancestor of . By replacing the current subway map with this tree, she believes it could reduce rush-hour congestion.
Task
Help Antonia generate the desired tree with the minimum number of nodes.
Input data
The input will contain a single integer number, – the number of pairs with the specified property.
Output data
The output will contain lines, representing the generated tree, the nodes being indexed from .
The first line will contain the number – the number of nodes in the tree.
The following lines will contain each 2 numbers and , separated by a space, with the following meaning: node is the direct ancestor of node . If node doesn’t have a direct ancestor, will have value .
Constraints and clarifications
- For each test, the tree must have at most nodes.
- For every test, you will get:
- points if
- points if
- points if , where
- Note: is the minimum number of nodes that a tree with the specified property can be generated with.
| # | Points | Constraints |
|---|---|---|
| 1 | 20 | |
| 2 | 30 | |
| 3 | 50 | No additional constraints |
Example 1
stdin
2
stdout
3
0 -1
1 0
2 0
Explanation
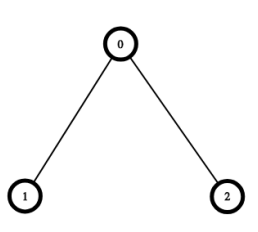
There are pairs , such that is the ancestor of :
Example 2
stdin
4
stdout
4
0 -1
1 0
2 0
3 2
Explanation
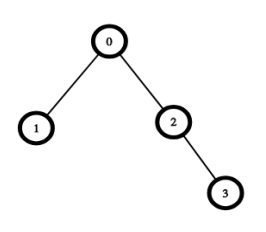
There are pairs , such that is the ancestor of :