O matrice pătratică de dimensiuni cu impar se numește matrice spirală dacă respectă următoarele proprietăți când este parcursă în spirală conform imaginii de mai jos:
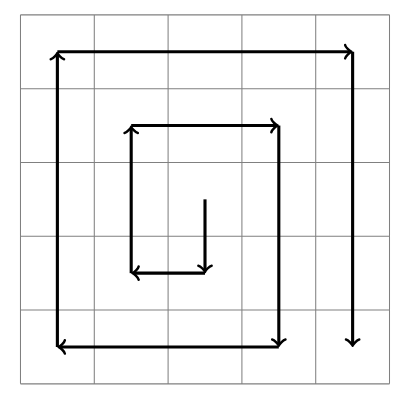
- Pentru oricare celulă din matrice, fie , fie nu conține cifra .
- Fie oricare celulă mai puțin cea din centru și celula parcursă anterior din matrice, și fie oricare cifră nenulă, adică de la la :
- a) Dacă divide , atunci conține cifra dacă și numai dacă nu conține cifra .
- b) Dacă nu divide , atunci conține cifra dacă și numai dacă conține cifra .
- c) Pentru numărul aflat în celula din centru, fiind prima parcursă, nu avem astfel de restricții.
- Un element din matrice va fi dacă și numai dacă acesta nu are voie să conțină nicio cifră de la la conform regulilor de mai sus.
Cerință
Dându-se o matrice pătratică de dimensiune , trebuie să determinați care este numărul minim de elemente din matrice care ar trebui înlocuite (în celulele respective pot fi scrise orice alte numere naturale) pentru ca să devină o matrice spirală.
Date de intrare
Pe prima linie a fișierului de intrare spirala.in se va afla un singur număr natural , reprezentând dimensiunile matricii. Pe următoarele linii se vor afla câte numere naturale separate prin câte un spațiu reprezentând elementele matricii .
Date de ieșire
Fișierul de ieșire spirala.out va conține un singur număr reprezentând minimul de elemente ce vor trebui înlocuite pentru ca să devină o matrice spirală.
Restricții și precizări
- , impar.
- Elementele matricii sunt numere naturale mai mici decât ce conțin doar cifre de la la , cu excepția elementelor egale cu .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 17 | Se poate obține o matrice spirală schimbând maxim un element din matricea |
| 2 | 23 | |
| 3 | 21 | |
| 4 | 39 | Fără restricții suplimentare |
Exemplu
spirala.in
5
16 36 1234 23456 145
26 1469 4569 123459 457
1236 269 13579 234579 12578
346 12569 359 135789 235789
13456 245 12457 578 45789
spirala.out
2
Explicație
Pentru a obține o matrice spirală, ar trebui înlocuite numerele din celulele și . În celula ar putea fi scris numărul și în celula , numărul .