Every four years, the students of Lund come together to organize the Lund Carnival. For a few days, a park fills with tents where all kinds of festive activities take place. The person in charge of making this happen is the carnival general.

In total, there have been $N$ carnivals, each with a different general. The generals are numbered from $0$ to $N − 1$ in chronological order. Every general $i$ has given their opinion on how good their predecessors were, by publishing a ranking of the generals $0, 1,…,i − 1$ in order from best to worst.

The next Lund Carnival will be in 2026. In the meantime, all past carnival generals have gathered to take a group photo. However, it would be awkward if generals $i$ and $j \ ($where $i < j)$ end up next to each other if $i$ is strictly in the second half of $j$'s ranking.

For example:

• If general $4$ has given the ranking 3 2 1 0, then $4$ can stand next to $3$, or $2$, but not $1$ or $0$.
• If general $5$ has given the ranking 4 3 2 1 0, then $5$ can stand next to $4, 3$ or $2$, but not $1$ or $0$. Note that it is fine if one general is exactly in the middle of another's ranking.

The following figure illustrates sample 1. Here, general $5$ stands next to generals $2$ and $3$, and general $4$ stands next to general $2$ only.

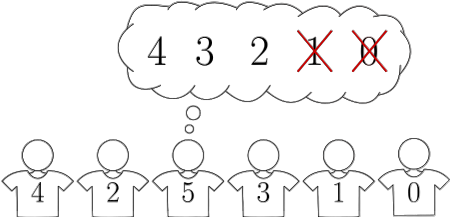
You are given the rankings that the generals published. Your task is to arrange the generals $0, 1,…, N − 1$ in a row, so that if $i$ and $j$ are adjacent $($where $i < j)$ then $i$ is not strictly in the second half of $j$'s ranking.

Input

The first line contains the positive integer $N$, the number of generals.

The following $N − 1$ lines contain the rankings. The first of these lines contains general $1$'s ranking, the second line contains general $2$'s ranking, and so on until general $N − 1$. General $0$ is absent since general $0$ didn't have any predecessors to rank.

The ranking of general $i$ is a list with $i$ integers $p_{i, 0}, p_{i, 1}, …, p_{i, i - 1}$ in which every integer from $0$ to $i − 1$ occurs exactly once. Specifically, $p_{i, 0}$ is the best and $p_{i, i - 1}$ is the worst general according to general $i$.

Print a list of integers, an ordering of the numbers $0, 1,…, N − 1$, such that for each pair of adjacent numbers, neither is strictly in the second half of the other's ranking.

It can be proven that a solution always exists. If there are multiple solutions, you may print any of them.

Constraints and Scoring

• $1 \leq N \leq 1 \ 000$
• $0 \leq p_{i, 0}, p_{i, 1}, ..., p_{i, i - 1} \leq i - 1$ for $i = 0, 1, ..., N - 1$

Your solution will be tested on a set of test groups, each worth a number of points. Each test group contains a set of test cases. To get the points for a test group, you need to solve all test cases in the test group.

Example 1

stdin

6
0
1 0
2 1 0
3 2 1 0
4 3 2 1 0

stdout

4 2 5 3 1 0

Explication

The first sample matches the condition of test group $1$. In this sample, neither general $2$ nor $3$ can stand next to general $0$, and neither general $4$ nor $5$ can stand next to generals $0$ and $1$. The sample output was illustrated in the figure above.

Example 2

stdin

5
0
0 1
0 1 2
0 1 2 3

stdout

2 0 4 1 3

Explication

The second sample matches the condition of test group $2$. In this sample, general $2$ can't stand next to general $1$, general $3$ can't stand next to general $2$, and general $4$ can't stand next to generals $3$ and $2$.

Example 3

stdin

4
0
1 0
0 2 1

stdout

3 0 1 2

Explication

The third sample matches the condition of test group $3$. In this sample, the only pairs of generals that can't stand next to each other are $(1, 3)$ and $(0, 2)$. Hence, there are no conflicts if they are arranged 3 0 1 2. Another possible answer is 0 1 2 3.