deminare

Pe un teren de formă dreptunghiulară format din $L$ linii și $C$ coloane sunt plantate $M$ mine. Liniile sunt numerotate de sus în jos cu valori de la $1$ la $L$ iar coloanele sunt numerotate de la stânga la dreapta cu valori de la $1$ la $C$.

Deoarece războiul s-a terminat, specialiștii vor să demineze terenul și să-l redea utilizării publice. Mutarea unei mine reprezintă operația de transfer a unei mine de la linia $x_1$ și coloana $y_1$ la o poziție liberă, dată de linia $x_2$ și coloana $y_2$, unde $1 \leq x_1,x_2 \leq L$ și $1 \leq y_1,y_2 \leq C$.

Deoarece mutarea unei mine este periculoasă, trebuie determinat numărul minim de mine care trebuie mutate din poziția inițială astfel încât toate minele de pe teren să fie așezate unele lângă altele într-o zonă compactă dreptunghiulară, oriunde în cadrul terenului dat, pentru ca apoi să fie detonate împreună.

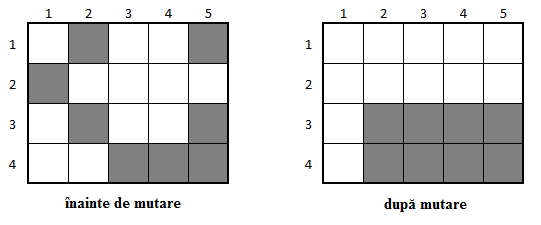
Spre exemplu: dacă $L=4$, $C=5$, $M=8$ și minele sunt așezate inițial conform figurii de mai jos (zonele colorate cu negru arată pozițiile minelor), pentru a se ajunge la o așezare a minelor într-o zonă compactă de formă dreptunghiulară numărul minim de mine mutate este $3$.

Cerințe

Cunoscând numărul de linii $L$ și de coloane $C$ ale terenului minat, numărul de mine $M$, precum și poziția fiecărei mine, să se scrie un program care determină:

1. linia sau liniile pe care se găsesc cele mai multe mine;
2. numărul minim de mine mutate, pentru ca toate minele de pe teren să fie așezate într-o zonă compactă cu formă dreptunghiulară.

Date de intrare

Fișierul de intrare este deminare.in și conține:

• pe prima linie numărul natural $V$ a cărui valoare poate fi doar $1$ sau $2$;
• pe a doua linie două numere naturale $L$ și $C$, cu semnificația din enunț;
• pe a treia linie numărul natural $M$, cu semnificația din enunț;
• pe fiecare din următoarele $M$ linii, câte o pereche de valori $x_i$ și $y_i$, $1 \leq i \leq M$, reprezentând linia, respectiv coloana, unde se află o mină.

Numerele aflate pe aceeași linie a fișierului sunt separate prin câte un spațiu.

Date de ieșire

Fișierul de ieșire este deminare.out.

Dacă valoarea lui $V$ este $1$ atunci prima linie a fișierului de ieșire va conține numărul liniei pe care se găsesc cele mai multe mine.
Dacă există două sau mai multe astfel de linii, se vor afișa toate numerele acestora, în ordine crescătoare, separate prin câte un spațiu.

Dacă valoarea lui $V$ este $2$ atunci fișierul de ieșire va conține pe prima linie numărul minim cerut de mine mutate. Dacă minele nu pot fi așezate într-o zonă compactă de formă dreptunghiulară, în fișierul de ieșire se va scrie valoarea $-1$.

Restricții și precizări

• $1 \leq L,C \leq 500$
• $1 \leq M \leq L \cdot C$
• O zonă în care se află mine așezate pe coloane consecutive, pe aceeași linie sau așezate pe linii consecutive, pe aceeași coloană se consideră că formează o zonă compactă de formă dreptunghiulară.
• O zonă compactă de formă dreptunghiulară poate avea numărul de linii ocupate egal cu numărul de coloane ocupate.
• Pentru teste valorând 20 de puncte, avem $V=1$.
• Pentru teste valorând 70 de puncte, avem $V=2$.
• Pentru teste valorând 20 de puncte, avem $V=2$ și $L \cdot C \leq 10\ 000$.
• Pentru teste valorând 32 de puncte, avem $V=2$ și $L \cdot C \leq 100\ 000$.

Exemplul 1

deminare.in

1
4 5
8
1 2
1 5
2 1
3 2
3 5
4 3
4 4
4 5

deminare.out

4

Explicație

Acest exemplu corespunde figurii din enunț.
$V=1$, deci se rezolvă doar cerința 1. $L=4$, $C=5$, $M=8$.

Minele sunt plasate la pozițiile $(1,2)$, $(1,5)$, $(2,1)$, $(3,2)$, $(3,5)$, $(4,3)$, $(4,4)$ și $(4,5)$.
Pe linia $1$ sunt amplasate 2 mine;
Pe linia $2$ este amplasată 1 mină;
Pe linia $3$ sunt amplasate 2 mine;
Pe linia $4$ sunt amplasate 3 mine.

Deci, există o singură linie pe care sunt amplasate un număr maxim de mine și anume linia $4$.

Exemplul 2

deminare.in

2
4 5
8
1 2
1 5
2 1
3 2
3 5
4 3
4 4
4 5

deminare.out

3

Explicație

Acest exemplu corespunde figurii din enunț.
$V=2$, deci se rezolvă doar cerința 2. $L=4$, $C=5$, $M=8$.

Minele sunt plasate la pozițiile $(1,2)$, $(1,5)$, $(2,1)$, $(3,2)$, $(3,5)$, $(4,3)$, $(4,4)$ și $(4,5)$.

Pentru a obține o zonă compactă de formă dreptunghiulară trebuie mutate minimum 3 mine. O variantă posibilă este:
Mina de la poziția $(1,2)$ se mută la poziția $(3,3)$;
Mina de la poziția $(1,5)$ se mută la poziția $(3,4)$;
Mina de la poziția $(2,1)$ se mută la poziția $(4,2)$.

Se obține o zonă compactă de formă dreptunghiulară, având colțul din stânga sus la poziția $(3,2)$ și colțul din dreapta jos la poziția $(4,5)$.