Se consideră puncte din plan, având coordonate numere naturale, relativ la un reper cartezian XOY, oricare două puncte fiind distincte.
Cerință
Cunoscând și coordonatele celor puncte, să se determine:
- Numărul maxim de puncte care au aceeași abscisă.
- Numărul triunghiurilor care se pot desena respectând următoarele condiții:
- au toate vârfurile în puncte dintre cele date;
- au o latură paralelă cu OX;
- nu au laturi paralele cu OY;
Date de intrare
Datele de intrare se citesc din fișierul triunghiuri.in, care are următoarea structură:
Pe prima linie se află numărul , care indică cerința ce trebuie rezolvată ( are valoarea sau );
Pe a doua linie se află numărul natural , reprezentând numărul punctelor date;
Pe următoarele linii se găsesc câte două valori naturale , separate prin câte un spațiu, reprezentând coordonatele punctelor date.
Date de ieșire
Fișierul triunghiuri.out va avea următoarea structură:
Dacă se va scrie în fișier, pe prima linie, numărul maxim de puncte care au aceeași abscisă (cerința ).
Dacă se va scrie în fișier, pe prima linie, numărul triunghiurilor care se pot desena respectând condițiile date, modulo , adică restul împărțirii numărului de triunghiuri la (cerința ).
Restricții și precizări
- ;
- ;
- Se acordă de puncte pentru rezolvarea corectă a cerinței și de puncte pentru rezolvarea corectă a cerinței .
Exemplul 1
triunghiuri.in
1
5
2 1
1 4
3 4
3 2
6 4
triunghiuri.out
2
Explicație
Se rezolvă cerința 1. Sunt maximum două puncte care au aceeași abscisă, () și ()
Exemplul 2
triunghiuri.in
2
5
2 1
1 4
3 4
3 2
6 4
triunghiuri.out
4
Explicație
Se rezolvă cerința . Se pot trasa triunghiuri care satisfac cerințele.
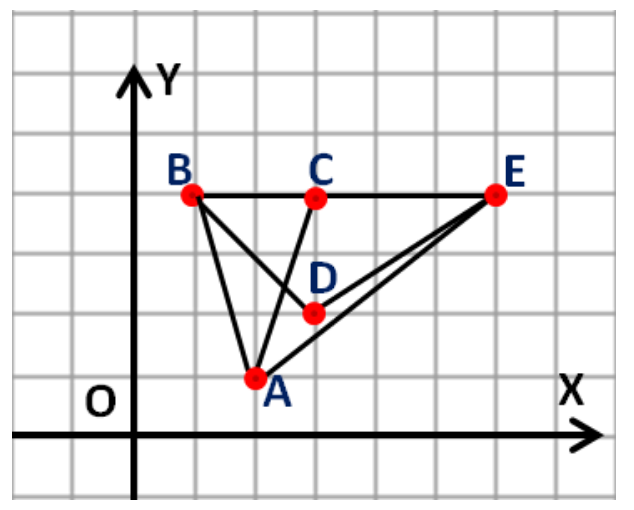
Dacă notăm cele puncte din fișier cu (ca în imagine),
atunci, cele triunghiuri care satisfac cerințele sunt: , , și .