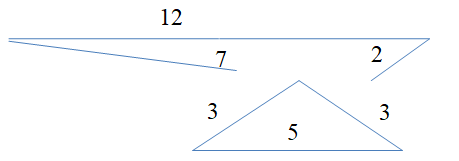
Gigel este un pasionat al triunghiurilor. El colectează beţişoare de diferite lungimi şi le asamblează în diferite triunghiuri. Ieri, el avea beţişoare de lungimi , , , , şi . Din aceste bețișoare, Gigel a construit un triunghi de laturi , şi , iar beţişoarele de lungimi , , au rămas nefolosite pentru că aceste lungimi nu pot forma laturile unui triunghi.
Din acest motiv, Gigel s-a hotărât să facă o colecţie de beţişoare, dintre care oricum ar alege elemente, acestea să nu poată forma laturile unui triunghi, proprietate pe care o vom numi în continuare proprietate anti-triunghi. Gigel, pornind de la setul iniţial de lungimi , s-a gândit la două metode de realizare a unei colecţii de beţişoare cu proprietatea anti-triunghi, şi anume:
- Păstrează cel mai scurt beţişor, cel de lungime , şi creează un set nou adăugând alte beţişoare de lungime mai mare sau egală cu cel iniţial. De exemplu, următoarele lungimi sunt corecte: .
- Păstreză toate beţişoarele, şi anume , pe care le va completa cu alte beţişoare de diferite lungimi (mai scurte sau mai lungi), astfel ca proprietatea anti-triunghi să se păstreze. Următoarele lungimi respectă proprietatea anti-triunghi: .
Cerinţă
Cunoscând un şir de numere naturale nenule având proprietatea anti-triunghi, şi un număr (), se cere să construiţi un şir de numere naturale având proprietatea anti-triunghi, în conformitate cu una dintre următoarele două restricţii
- Varianta 1: Cel mai mic element este identic cu cel mai mic element din şirul iniţial.
- Varianta 2: Printre cele elemente ale şirului construit se regăsesc toate elementele şirului iniţial.
Date de intrare
Fişierul de intrare triunghi.in conţine pe prima linie valorile numerelor şi , separate prin spaţiu. Linia următoare conţine numere naturale separate prin spaţiu, ce formează un şir cu propietatea anti-triunghi.
Date de ieșire
Fişierul de ieşire triunghi.out va conţine numere pe o singură linie.
Dacă valoarea lui este , atunci fişierul va conţine numere naturale cu proprietatea anti-triunghi, separate prin spaţiu, în care cel mai mic element este identic cu minimul şirului dat în fişierul de intrare.
Dacă valoarea lui este , atunci fişierul va conţine numere naturale cu proprietatea anti-triunghi, separate prin spaţiu, printre care se regăsesc toate elementele şirului iniţial.
Restricții și precizări
- lungimea unui beţişor
- Pentru rezolvarea corectă a primei cerinţe se acordă de puncte, iar pentru cerinţa a doua se acordă de puncte.
- Se garantează că întotdeauna există soluţie.
- Soluţia nu este unică - se admite orice răspuns corect.
Exemplul 1
triunghi.in
1 3 5
7 2 12
triunghi.out
2 2 30 50 12
Explicație
, , .
În varianta avem de tipărit numere, valoarea minimului este în ambele şiruri.
Exemplul 2
triunghi.in
2 3 5
7 2 12
triunghi.out
1 4 12 7 2
Explicație
, , .
În varianta printre elementele şirului tipărit se regăsesc toate elementele şirului iniţial.