Fascinat de Egiptul Antic, Rareș vrea să construiască cât mai multe piramide din cartonașe pătratice identice. El are la dispoziție cartonașe numerotate de la la , albe sau gri, așezate în ordinea strict crescătoare a numerelor.
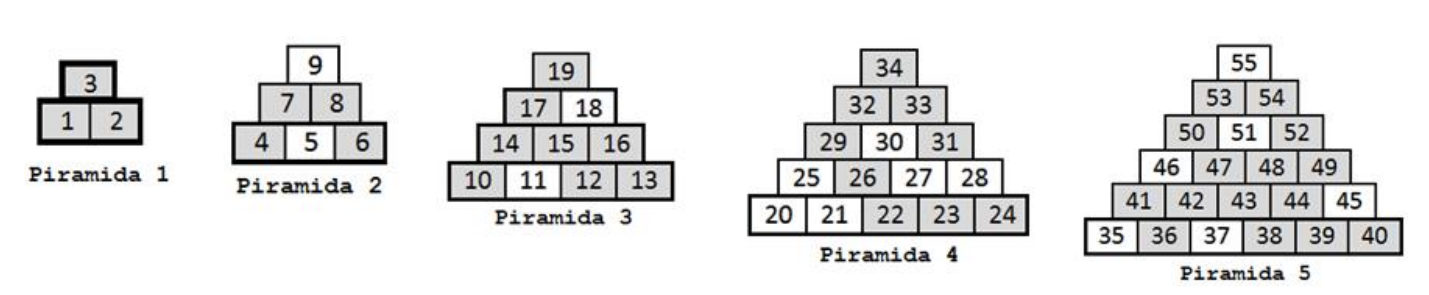
Prima piramidă o va construi folosind primele trei cartonașe. Baza piramidei va fi formată din cartonașele și așezate alăturat, peste care va așeza cartonașul (vârful piramidei).
A doua piramidă va avea baza formată din cartonașele , și așezate alăturat, deasupra cărora se vor așeza cartonașele și , alăturate, peste care se va așeza cartonașul (vârful piramidei).
Mai departe, va construi în ordine piramidele complete cu bazele formate din cartonașe (cu numerele de la la ), respectiv cartonașe (cu numerele de la la ), cartonașe (cu numerele de la la ) etc., cât timp va putea construi o piramidă completă. De exemplu, dacă Rareș are cartonașe atunci el va construi piramidele complete , , , și din imaginile următoare. Din cele de cartonașe el va folosi doar primele de cartonașe, deoarece ultimele cartonașe nu sunt suficiente pentru a construi piramida , cu baza formată din cartonașe.
Cerință
Scrieți un program care să citească numerele naturale (reprezentând numărul de cartonașe), (reprezentând numărul unui cartonaș), (reprezentând numărul de cartonașe albe), numerele celor cartonașe albe , , ..., și care să determine:
- numărul al piramidei complete ce conține cartonașul numerotat cu ;
- numărul maxim de piramide complete construite de Rareș;
- numărul de cartonașe nefolosite;
- numărul al primei piramide complete care conține cele mai multe cartonașe albe.
Date de intrare
Fișierul de intrare piramide.in conține pe prima linie cele trei numere , și , separate prin câte un spațiu, cu semnificația din enunț. A doua linie a fișierului conține, în ordine, cele numere , , ..., , separate prin câte un spațiu, reprezentând numerele celor cartonașe albe din cele .
Date de ieșire
Fișierul de ieșire piramide.out va conține pe prima linie numărul sau valoarea (zero) dacă niciuna dintre piramidele complete construite nu conține cartonașul cu numărul .
A doua linie a fișierului va conține numărul .
Cea de-a treia linie va conține numărul .
Cea de-a patra linie va conține numărul sau valoarea (zero) dacă nicio piramidă completă nu conține cel puțin un cartonaș alb.
Restricții și precizări
- ;
- ;
- ;
- ;
- O piramidă completă cu baza formată din cartonașe se construiește prin așezarea cartonașelor necesare pe rânduri: cartonașe pe primul rând (al bazei), apoi cartonașe pe rândul al doilea, pe rândul al treilea, , două cartonașe pe rândul și un cartonaș (vârful piramidei) pe rândul .
- Pentru rezolvarea cerinței a) se acordă 20% din punctaj, pentru cerința b) 20% din punctaj, pentru cerința c) 20% din punctaj și pentru cerința d) 40% din punctaj.
Exemplu
piramide.in
75 15 23
5 9 11 18 20 21 25 27 28 30 35 37 45 46 51 55 60 65 68 69 70 71 72
piramide.out
3
5
20
4
Explicație
Piramida () construită conține cartonașul cu numărul . Rareș poate construi doar piramide complete, rămânând nefolosite cartonașe () insuficiente pentru construirea piramidei . Numărul maxim de cartonașe albe dintr-o piramidă completă este egal cu . Piramidele și conțin fiecare un număr maxim de cartonașe albe (), prima dintre acestea fiind piramida (). Ultimele cartonașe albe (cu numerele: , , , , , , ) nu sunt folosite în construirea piramidelor complete.