Se consideră un text memorat într-o matrice , definită prin coordonatele colţului stânga sus şi coordonatele colţului dreapta jos .
Prin aplicarea unui algoritm de compresie, matricei i se asociază un şir de caractere, notat .
Şirul de caractere este construit prin aplicarea următoarelor reguli:
a) dacă matricea are o singură linie şi o singură coloană atunci conţine numai caracterul memorat în matrice
b) dacă toate elementele matricei sunt identice atunci întreaga matrice se comprimă şi este şirul , unde reprezintă numărul de caractere din matrice, iar caracterul memorat
c) dacă matricea este formată din caractere diferite şi are cel puţin două linii şi două coloane atunci:
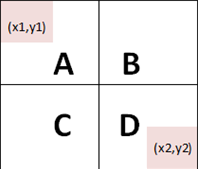
- matricea este împărţită în submatrice , , , după cum este ilustrat în figura alăturată, unde coordonatele colţului stânga sus ale submatricei sunt , iar coordonatele colţului dreapta jos sunt
- este şirul
*, unde , , , sunt şirurile de caractere obţinute, în ordine, prin compresia matricelor , , , utilizând acelaşi algoritm
d) dacă matricea este formată din caractere diferite, are o singură linie şi mai multe coloane atunci este şirul * , unde , , , au semnificaţia descrisă la punctul c).
e) dacă matricea este formată din caractere diferite, are mai multe linii şi o singură coloană atunci este şirul * unde , , , au semnificaţia descrisă la punctul c).
Cerinţă
Dat fiind şirul de caractere ce se obţine în urma aplicării algoritmului de compresie asupra unei matrice de dimensiune să se determine:
a) numărul de împărţiri care au fost necesare pentru obţinerea textului compresat
b) matricea iniţială din care provine textul compresat.
Date de intrare
Fişierul de intrare compresie.in conţine pe prima linie un şir de caractere ce reprezintă textul compresat.
Date de ieșire
Fişierul de ieșire compresie.out conţine:
- pe prima linie un număr natural ce reprezintă numărul de împărţiri care au fost necesare pentru obţinerea textului compresat
- pe următoarele linii se găsesc câte caractere, litere mici ale alfabetului englez, neseparate prin spații, ce reprezintă, în ordine, liniile matricei iniţiale.
Restricții și precizări
- lungimea şirului compresat
- Textul memorat iniţial în matricea conţine numai caractere din mulţimea literelor mici
abz. - Pentru rezolvarea corectă a cerinţei a) se acordă din punctaj, iar pentru rezolvarea corectă a ambelor cerinţe se acordă tot punctajul.
Exemplul 1
compresie.in
*4b*bbab4a*abbb
compresie.out
3
bbbb
bbab
aaab
aabb
Explicație
Au fost efectuate împărţiri:
Exemplul 2
compresie.in
*4a*ab*aba
compresie.out
3
aaa
aab
aba
Explicație
Au fost efectuate împărţiri: