Zarul folosit la diverse jocuri este un cub care are desenat pe fiecare față a sa sau puncte. Pe un zar nu există două fețe cu același număr de puncte și suma punctelor de pe oricare două fețe opuse este egală cu .
Pe o masă de joc este desenat un traseu în formă de pătrat, cu latura de dimensiune . Fiecare latură a traseului este împărțită în pătrățele identice, care au latura egală cu cea a zarului. Zarul este așezat inițial în colțul din stânga sus al traseului și apoi rostogolit de pe o față pe alta, din pătrățel în pătrățel, de-a lungul traseului parcurs în sensul acelor de ceasornic.
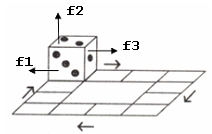
În orice moment ne-am uita la zar, putem vedea numărul punctelor desenate pe trei din fețele sale (așa cum se vede în desenul de mai sus).
Notăm cu fața cubului orientată spre noi, fața superioară a cubului, respectiv cu fața laterală din dreapta. Pentru exemplul din figură: , fața dinspre noi () conține trei puncte, fața superioară () conține două puncte, fața laterală din dreapta () conține un punct, iar sensul de deplasare este cel precizat prin săgeți.
Cerință
Cunoscând dimensiunea a traseului și numărul punctelor de pe cele trei fețe ale zarului în poziția inițială, determinați după rostogoliri numărul punctelor ce se pot observa pe fiecare din cele trei fețe ale zarului.
Date de intrare
Fișierul zar.in conține pe prima linie numerele naturale și despărțite printr-un spațiu. Pe linia a doua se află trei numere naturale separate prin spații ce corespund numărului de puncte de pe fețele , respectiv ale zarului în poziția inițială.
Date de ieșire
Fișierul zar.out va conține o singură linie cu trei numere naturale separate prin câte un spațiu, care reprezintă numărul punctelor ce se pot observa pe fețele , și (în această ordine) după ce au fost efectuate rostogoliri pe traseul dat.
Restricții și precizări
Exemplu
zar.in
4 11
3 2 1
zar.out
1 5 3
Explicație
Fiecare latură a traseului este formată din căsuțe și se vor efectua rostogoliri. După prima rostogolire spre dreapta, valorile celor trei fețe (, respectiv ) ale zarului vor fi și . După a doua rostogolire obținem numerele , iar după a treia rostogolire valorile fețelor vor fi și . În acest moment zarul a parcurs o latură a traseului. Următoarele trei rostogoliri se vor efectua în jos, de-a lungul traseului iar fețele vor avea succesiv valorile apoi și . Urmează rostogolirile spre stânga, pe fețele zarului vom observa valorile apoi și respectiv . Ultimele două rostogoliri se vor efectua în sus de-a lungul laturii din stânga a traseului. După penultima rostogolire obținem , iar după ultima rostogolire valorile fețelor vor fi și .