ashima

Se dă un șir $A$, ale cărui elemente sunt definite prin relația $A_i$ = $i^K \cdot 2^i$ pentru orice $1 \leq i$, unde $K$ este un număr natural dat. Elementele acestui șir se așează într-o matrice $M$, formată din $L$ linii și $C$ coloane, astfel: $M_{11} = A_1$, $M_{21} = A_2$, $M_{12} = A_3$, $M_{31} = A_4$, $M_{22} = A_5$, $M_{13} = A_6$, $M_{41} = A_7$, $M_{32} = A_8$ ..., adică parcurgând matricea pe diagonale din stânga-jos spre dreapta-sus.

De exemplu, pentru $K=0$, $L=3$ și $C=4$, șirul $A$ este format din elementele $2, 4, 8, 16, 32, 64...$, iar matricea $M$ va fi completată astfel:

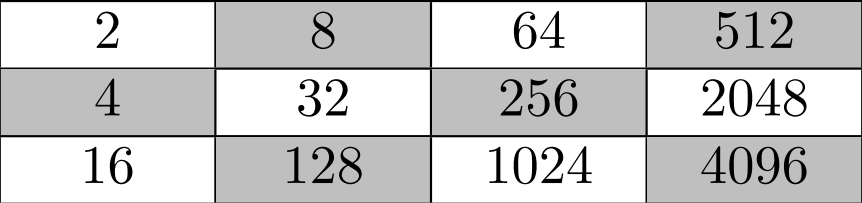
Cerință

Ashima vă cere să răspundeți la $Q$ cerințe de forma:

• $l_1 \ l_2 \ c_1 \ c_2$ : care este suma elementelor $M_{ij}$ din matricea $M$ astfel încât $l_1 \leq i \leq l_2$ și $c_1 \leq j \leq c_2$?

Date de intrare

Pe prima linie a fișierului de intrare se află numerele $K$, $L$, $C$ și $Q$, iar pe următoarele $Q$ linii se află câte patru numere $l_1 \ l_2 \ c_1 \ c_2$.

Date de ieșire

În fișierul de ieșire se vor afișa $Q$ linii. Pe linia $i$ se va afișa rezultatul celei de a $i$-a cerințe, modulo $1 \ 000 \ 000 \ 007$.

Restricții

• $0 \leq K \leq 3$
• $1 \leq L,C \leq 100 \ 000$
• $1 \leq Q \leq 200$
• $1 \leq l_1 \leq l_2 \leq L$
• $1 \leq c_1 \leq c_2 \leq C$
• $0 \leq l_2 - l_1, c_2 - c_1 \leq 1 \ 000$

Exemplul 1

ashima.in

0 3 4 3
1 1 2 4
1 2 1 3
1 3 2 3

ashima.out

584
366
1512

Explicație

Pentru acest exemplu matricea $M$ se completează ca în exemplul dat în enunț.

• La prima cerință trebuie calculată suma elementelor aflate între liniile $1$ și $1$ și coloanele $2$ și $4$. Suma acestor elemente este $8 + 64 + 512 = 584$.
• La a doua cerință trebuie calculată suma elementelor aflate între liniile $1$ și $2$ și coloanele $1$ și $3$. Suma acestor elemente este $2 + 8 + 64 + 4 + 32 + 256 = 366$.
• La a treia cerință trebuie calculată suma elementelor aflate între liniile $1$ și $3$ și coloanele $2$ și $3$. Suma acestor elemente este $8 + 64 + 32 + 256 + 128 + 1024 = 1512$.

Exemplul 2

ashima.in

1 2 5 2
1 1 2 4
1 2 1 3

ashima.out

1080
642

Explicație

Pentru acest exemplu avem $K = 1$, deci șirul $A$ are elementele $1 \cdot 2^1$, $2 \cdot 2^2$, $3 \cdot 2^3$, ..., $10 \cdot 2^{10}$, iar matricea $M$, cu $2$ linii și $5$ coloane se completează astfel:

• La prima cerință trebuie calculată suma elementelor aflate între liniile $1$ și $1$ și coloanele $2$ și $4$. Suma acestor elemente este $24 + 160 + 896 = 1080$.
• La a doua cerință trebuie calculată suma elementelor aflate între liniile $1$ și $2$ și coloanele $1$ și $3$. Suma acestor elemente este $2 + 24 + 160 + 8 + 64 + 384 = 642$.

Dacă ați reușit să răspundeți la cerințe, șirul $\textbf{A shi}$ matricea $\textbf{Ma}$ vă mulțumesc pentru ajutor!