Enunț
Definim un număr natural “tablou” dacă și numai dacă:
- este compus;
- Există și numere naturale, astfel încât cu proprietatea că există o matrice de forma dreptunghiulară cu lățimea si lungimea , astfel încât suma oricăror numere este pozitivă și există numere, astfel încât suma celor numere este divizibilă cu ;
- Fiecare număr din coordonatele va fi sub forma: ;
- Liniile vor fi numerotate de la la , iar coloanele vor fi numerotate de la la ;
De exemplu, 25 este un număr “tablou”, deoarece pot forma matricea de formă dreptunghiulară cu lățimea 5 și lungimea 5, arătând astfel:
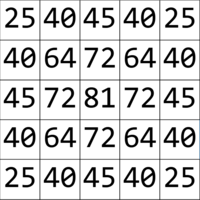
Oricum am alege numere din matricea respectivă, suma celor 5 numere va fi pozitivă și există cele numere , , , și , ale căror sumă este , deci suma a celor numere se divide cu .
Fiind dat numărul și pe următoarele linii câte un număr , să se afișeze dacă este un număr “tablou”, respectiv dacă nu este un număr “tablou”.
Cerință
Dat numărul natural și pe următoarele linii câte un număr , să se afișeze dacă respectă proprietatea din enunț, respectiv dacă nu respectă proprietatea din enunț.
Date de intrare
În fișierul tablou.in se va afla numărul pe prima linie, iar pe următoarele linii se va afla câte un număr natural .
Date de ieșire
În fișierul tablou.out se va afla mesajul dacă numărul este un număr “tablou”, respectiv dacă numărul nu este un număr “tablou”.
Restricții și precizări
- Pentru 25 de puncte, și
- Pentru 4 puncte, fiecare X din fișierul de intrare nu este compus
- 1 nu se ia în considerare ca număr compus
Exemplu:
tablou.in
3
25
13
18
tablou.out
DA
NU
NU
Explicații:
25 este un număr “tablou”, deoarece există matricea de formă dreptunghiulară cu lățimea 5 și lungimea 5 care are proprietatea specificată din enunț.
13 nu este un număr ”tablou”, deoarece nu este compus.
18 nu este un număr “tablou”, deoarece nu există o matrice de formă dreptunghiulară care are proprietatea specificată în enunț.