John și-a investit toate economiile în criptomonede. Acum încearcă să mai recupereze din bani, trecând pe dieta campionilor (brânză topită).
El are o cutie circulară cu bucăți de brânză (de mai multe tipuri), iar în fiecare zi ia câte una din cutie. Acesta are grijă ca înainte și după ce ia o bucată din cutie, oricare două bucăți adiacente rămase să fie de alt tip.
John s-a apucat să numere în câte moduri poate să termine cutia.
Formal, se dă un vector circular . Vrem să scoatem din el câte un element până rămâne gol vectorul. În urma fiecărei scoateri, inclusiv înaintea primei scoateri, nu trebuie să existe 2 poziții consecutive în vector cu aceeași valoare în ele.
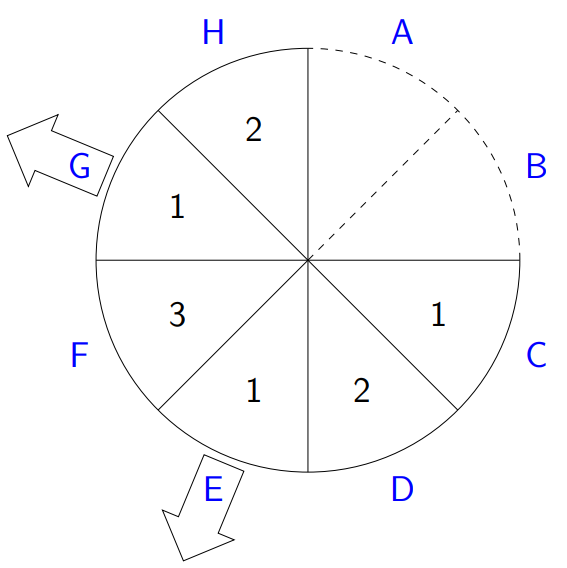
În exemplul din dreapta, bucățile de brânză de pe pozițiile și au fost deja luate. Singurele bucăți pe care le-am putea scoate acum ar fi sau . Dacă am scoate bucata , atunci bucățile si , ambele de tipul , ar deveni vecine. Dacă l-am scoate pe , și ar deveni vecine, deși sunt ambele de tipul , etc.
Cerință
Să se numere în câte moduri putem goli vectorul respectând regulile din enunț (modulo ).
Un mod de a goli vectorul este definit de ordinea indicilor care părăsesc vectorul. De exemplu, pentru , sunt de moduri diferite de a goli vectorul (dintre care nu toate respecța regulile din enunț).
Date de intrare
Pe prima linie a fișierului de intrare se găsește un singur număr natural reprezentând lungimea vectorului.
Pe a doua linie se găsesc numere naturale, , reprezentând valorile din vector.
Date de ieșire
În fişierul de ieşire se va afişa un singur număr, reprezentând numărul de moduri de a goli vectorul.
Problema are 2 moduri de punctare: vectorul este circular (pentru din punctajul de pe un test), sau vectorul nu este circular – și nu sunt considerați vecini (pentru din punctaj).
Inițial, numărul afișat este comparat cu răspunsul corespunzător vectorului circular pentru din punctajul testului.
Dacă răspunsurile diferă, numărul este apoi comparat cu răspunsul corespunzător vectorului normal ( și nu sunt considerați vecini) pentru din punctajul testului.
Restricții
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 10 | |
| 2 | 10 | |
| 3 | 30 | |
| 4 | 50 | Fără restricții suplimentare |
Exemple
bt.in
4
1 2 1 2
bt.out
0
Orice element am scoate, am avea ulterior doi de vecini, sau doi de vecini, deci nu putem goli vectorul. Dacă am avea un delimitator între ultimul element și primul, răspunsul ar fi . Secvențele de indici corecte în acest caz ar fi:
- , , ,
- , , ,
- , , , (vectorul ar arăta: gol)
- , , ,
- , , ,
- , , ,
- , , ,
- , , ,
bt.in
8
1 2 1 3 1 2 1 3
bt.out
1728
Răspunsul corect dacă ar exista un delimitator este .
bt.in
4
1 2 3 4
bt.out
24
Deoarece orice element din vector este distinct, acestea pot fi scoase în orice ordine. Răspunsul pentru celălalt caz este tot .
bt.in
6
1 2 3 1 3 2
bt.out
96
Răspunsul corect dacă ar exista un delimitator este .
bt.in
1
1
bt.out
1
Avem un singur element în vector, deci există o singură cale de a-l scoate. Răspunsul pentru celălalt caz este tot .