balon

Firma TgM produce plăci de umflat baloane. O placă de dimensiuni $n$ x $m$ este formată din $n$ linii cu câte $m$ celule pătrate de latură $1$, fiecare celulă conținând un dispozitiv de care poate fi prins un balon pentru a fi umflat. Un balon are un nivel de umplere $b_i{}_j$ cuprins între $1$ (dezumflat) și nivelul de umplere maxim posibil $k$. Introducerea unui nou volum de aer într-un balon umplut la nivelul maxim $k$, conduce la spargerea lui (nivel $k+1$). Fiecare balon spart este înlocuit automat cu un balon nou aflat la nivelul de umplere $1$ înainte de a introduce un nou volum de aer în oricare dintre baloanele de pe placă.
Introducerea aerului în anumite baloane se face printr-o acționare care constă în următorii pași:

• se conectează un sistem cilindru-piston la dispozitivul dintr-o celulă aflată pe linia $x$ și coloana $y$;
• se selectează o valoare naturală nenulă $d$;
• se apasă butonul Air aflat pe mânerul pistonului.

În urma acționării butonului Air, fiecare balon situat în pătratul cu colțul din stânga sus ($x$, $y$) cu latura $d$ trece de la nivelul de umplere curent la nivelul de umplere imediat următor. Dacă pătratul de latură $d$ depășește una sau mai multe din marginile plăcii, se transmite aer doar în baloanele aflate în interiorul acestuia. La acționarea butonului se consumă un număr de unități de volum de aer egal cu numărul de baloane aflate în interiorul pătratului.

Cerințe

Dându-se dimensiunile unei plăci $n$ și $m$, nivelul maxim posibil de umplere a unui balon $k$, numărul $p$ de acționări ale butonului Air, nivelul inițial de umplere al fiecărui balon de pe placă și pentru fiecare dintre acționările pistonului cele trei valori $x$, $y$ și $d$ corespunzătoare, scrieți un program care determină și afișează:

1. numărul de unități de aer consumate după cele $p$ acționări ale butonului Air;
2. numărul de baloane sparte după cele $p$ acționări ale butonului Air;
3. nivelul maxim de umplere a unui balon după cele $p$ acționări ale butonului Air și numărul de baloane aflate la acest nivel de umplere.

Date de intrare

Fișierul de intrare balon.in conține pe prima linie un număr natural $C$, reprezentând cerința ce trebuie rezolvată ($1$, $2$ sau $3$), pe a doua linie patru numere naturale nenule $n$, $m$, $k$ și $p$, cu semnificația din enunț, pe fiecare din următoarele $n$ linii câte $m$ valori reprezentând nivelul inițial de umplere a baloanelor de pe linia respectivă, iar pe fiecare din ultimele $p$ linii câte trei numere naturale $x$, $y$ și $d$ corespunzătoare unei acționări a pistonului.
Numerele aflate pe aceeași linie a fișierului sunt separate prin câte un spațiu.

Date de ieșire

In fișierul de ieșire balon.out:

• dacă $C = 1$, se va afișa pe prima linie numărul de unități de aer consumate după cele $p$ acționări ale butonului Air;
• dacă $C = 2$, se va afișa pe prima linie numărul de baloane sparte după cele $p$ acționări ale butonului Air;
• dacă $C = 3$, se vor afișa pe prima linie două numere separate printr-un spațiu reprezentând nivelul maxim de umplere a unui balon după cele $p$ acționări ale butonului Air și numărul de baloane aflate la acest nivel de umplere.

Restricții și precizări

• $C \in \{1, 2, 3\}$;
• $1 \leq n, m, d \leq 1 \ 000$;
• $1 \leq x \leq n$ și $1 \leq y \leq m$;
• $3 \leq k, p \leq 1 \ 000 \ 000$;
• $1 \leq b_i{}_j \leq k$, pentru oricare $1 \leq i \leq n$ și $1 \leq j \leq m$;
• Pentru $30$ de puncte, $C = 1$;
• Pentru $35$ de puncte, $C = 2$;
• Pentru $35$ de puncte, $C = 3$.

Exemplul 1

balon.in

1
4 6 5 2
1 2 3 3 2 1
1 1 4 3 2 2
3 1 1 1 5 3
2 4 2 4 2 2
2 1 3
3 5 3

balon.out

13

Explicație

$C = 1$, $n = 4$, $m = 6$, $k = 5$ și $p = 2$.
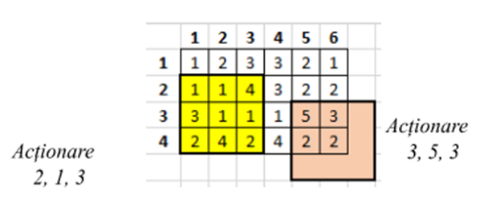
La prima acționare a pistonului se consumă $9$ unități de volum de aer corespunzătoare elementelor marcate cu galben în figura din enunț.
La a doua acționare a pistonului se consumă $4$ unități de volum de aer corespunzătoare elementelor marcate cu roz în figura din enunț, deoarece doar patru dintre baloane sunt în interiorul pătratului de latură $3$ cu colțul din stânga sus în poziția $(3, 5)$.

Exemplul 2

balon.in

2
4 6 5 3
1 2 3 3 2 1
1 1 4 3 2 2
3 1 1 1 5 3
2 4 2 4 2 2
2 1 3
3 5 3
3 2 4

balon.out

2

Explicație

$C = 2$, $n = 4$, $m = 6$, $k = 5$ și $p = 3$.

După prima acționare corespunzătoare tripletei $x=2$, $y=1$, $d=3$ nivelurile de umplere devin:

și nu s-a spart niciun balon.

După a doua acționare corespunzătoare tripletei $x=3$, $y=5$, $d=3$ nivelurile de umplere devin:

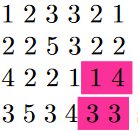
și s-a spart balonul din poziția $x=3$, $y=5$, fiind înlocuit automat cu un balon nou.

După a treia acționare corespunzătoare tripletei $x=3$, $y=2$, $d=4$ nivelurile de umplere devin:

și s-a spart balonul din poziția $x=4$, $y=2$, fiind înlocuit automat cu un balon nou. În total s-au spart $2$ baloane.

Exemplul 3

balon.in

3
4 6 5 3
1 2 3 3 2 1
1 1 4 3 2 2
3 1 1 1 5 3
2 4 2 4 2 2
2 1 3
3 5 3
3 2 4

balon.out

5 2

Explicație

$C = 3$, $n = 4$, $m = 6$, $k = 5$ și $p = 3$.
După cele trei acționări, nivelurile de umplere au devenit:

1 2 3 3 2 1
2 2 5 3 2 2
4 3 3 2 2 4 
3 1 4 5 4 3

Nivelul maxim de umplere a unui balon este $5$ și sunt două baloane cu acest nivel de umplere.