arcade

Ernest a găsit în garajul familiei sale un joc Pacman. Labirintul din joc poate fi reprezentat ca o matrice cu $N$ linii și $N$ coloane. Pe fiecare linie și fiecare coloană există exact un obstacol. Vom nota cu $(L, C)$ poziția de pe linia $L$ și coloana $C$.
Matricea este circulară: dacă Pacman se deplasează la dreapta din poziția $(L, N)$, ajunge în $(L, 1)$, iar dacă se deplasează la stanga din poziția $(L, 1)$, ajunge în $(L, N)$, pentru orice linie $L$ din matrice. Similar, dacă se deplasează în sus din $(1, C)$, ajunge în $(N, C)$, respectiv dacă se deplasează în jos din $(N, C)$, ajunge în $(1, C)$, pentru orice coloană $C$. Inițial Pacman se află în $(1, 1)$ și vrea sa ajungă în $(N, N)$ unde se găse ște un punct galben care îl va ajuta să învingă fantomele colorate.
Regulile acestei versiuni de joc permit doar $4$ tipuri de mișcări pentru Pacman, relative la poziția curentă:

• U - se deplasează în sus până se lovește de un obstacol sau a ajuns în $(N, N)$.
• D - se deplasează în jos până se lovește de un obstacol sau a ajuns în $(N, N)$.
• L - se deplasează la stânga până se lovește de un obstacol sau a ajuns în $(N, N)$.
• R - se deplasează la dreapta până se lovește de un obstacol sau a ajuns în $(N, N)$.

De remarcat faptul că, odată ajuns în $(N, N)$, Pacman nu va mai putea părăsi această poziție, indiferent de mișcările ulterioare pe care le-ar face.

Cerință

Problema este formată din doua cerințe:
Cerința 1. Se citește un șir de mișcări format din literele U, D, L, R, ce descriu în ordine mișcările lui Pacman. Deplasându-se conform acestui șir, va ajunge Pacman din $(1, 1)$ la punctul galben de coordonate $(N, N)$?
Cerința 2. Care este numărul minim de mișcări U, D, L, R prin care Pacman poate ajunge din $(1, 1)$ la punctul galben de coordonate $(N, N)$?

Date de intrare

Fiecare fișier de intrare va conține $T$ teste.
Pe prima linie a fișierului se află numărul cerinței $C \in \{1, 2\}$ și numărul de teste $T$. Pe prima linie a fiecărui test $i$ se află $N_i$, dimensiunea matricei pentru testul $i$, iar pe a doua linie sunt $N_i$ numere $P_1$, $P_2$, ..., $P_{N_i}$ . Pentru fiecare $1 \leq j \leq N_i$, obstacolul $j$ are coordonatele $(j, P_j)$. Dacă $C = 1$, pe a treia linie a fiecărui test se află mișcările scrise ca un șir de caractere, fără spații, din mulțimea $\{U, D, L, R\}$.

Date de ieșire

Pe fiecare dintre cele $T$ linii ale fișierului de ieșire se va afla răspunsul pentru testul corespunzător. În cazul în care $C = 1$, se va afișa "Won", dacă răspunsul la cerin ță este afirmativ, respectiv "Lost", dacă răspunsul este negativ. Dacă $C = 2$, se va afișa numărul minim de mișcări cerut, sau $−1$ dacă nu se poate ajunge din $(1, 1)$ în $(N, N)$.

Restricții și precizări

• $1 \leq T \leq 5 * 10^4$;
• $2 \leq N_i$, pentru orice test $1 \leq i \leq T$;
• Suma tuturor valorilor $N_i$, pentru $1 \leq i \leq T$, este $\leq 10^5$;
• $1 \leq P_j \leq N_i$ și $P_j \neq P_k$ pentru orice $j \neq k$.
• Pentru $C = 1$, suma lungimilor șirurilor de mișcări din toate cele $T$ teste nu depășește $1 \ 000 \ 000$.
• Se garantează că $(1, 1)$ și $(N, N)$ nu sunt blocate de un obstacol ($P_1 \neq 1$ și $P_N \neq N$).

Exemplul 1

arcade.in

1 3
5
2 1 3 5 4
LDLDL
4
3 1 4 2
RDRUL
6
3 2 1 6 5 4
RURU

arcade.out

Won
Lost
Won

Explicație

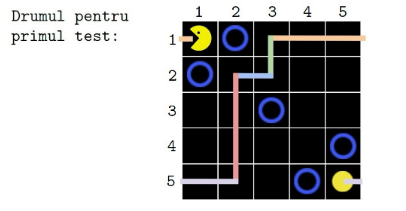
Exemplul 2

arcade.in

2 3
5
2 1 3 5 4
6
6 5 4 3 2 1
6
3 2 1 6 5 4

arcade.out

4
-1
4

Explicație