Ranuto are un program de antrenament de-a lungul a mai multor zile, în care vrea să învețe o nouă tehnică: “11th Gate Super Convincing Chakra Dual-Core Rasengan”. Din motive obiective, vrea să știe din avans în ce ar putea consta antrenamentul lui într-o zi anume (vine Kasura să se uite la el).
Se dă un arbore cu noduri, numerotate de la la . Arborele este înrădăcinat în nodul .
Vrem să facem o parcurgere a arborelui, pornind din rădăcină. Pentru fiecare nod, putem considera fiii acestuia în orice ordine dorim.
Există două tipuri de cerințe, reprezentate printr-un număr :
- Pentru , parcurgerea va fi de tip adâncime (DFS) pre-ordine;
- Pentru , parcurgerea arborelui va fi de tip lățime (BFS).
Pseudocodul pentru parcurgeri poate fi consultat mai jos:
Algoritmul 1 Parcurgere în adâncime (DFS) pre-ordine
- p listă goală (va conține nodurile din parcurgere)
- procedură DFS(arbore, nod):
- adaugă nod în spatele lui p
- pentru fiecare fiu x al lui nod:
- DFS(arbore, x)
- DFS(arbore, 1)
Algoritmul 2 Parcurgere în lățime (BFS)
- p listă goală (va conține nodurile din parcurgere)
- procedură BFS(arbore):
- q coadă goală
- adaugă nodul 1 în spatele lui q
- cât timp q nu este goală:
- f nodul din fața lui q
- scoate f din fața lui q
- adaugă f în spatele lui p
- pentru fiecare fiu x al lui f:
- adaugă nodul x în spatele lui q
- BFS(arbore)
Cerință
Care noduri din arbore pot să fie pe a -a poziție în vreuna dintre posibilele parcurgeri?
Date de intrare
Pe prima linie se găsesc trei numere, , și . Pe următoarele linii se găsesc câte numere, și , semnificând existența unei muchii în arbore între nodurile și .
Date de ieșire
Afișați pe o linie, cu un spațiu între ele, în ordine crescătoare, toate nodurile care pot fi pe a -a poziție în vreo parcurgere de tipul stabilit de . Nu trebuie afișat numărul de noduri.
Restricții și precizări
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 5 | , |
| 2 | 5 | , |
| 3 | 5 | . Arborele este binar complet, cu de forma , număr natural nenul |
| 4 | 5 | . Arborele este binar complet, cu de forma , număr natural nenul |
| 5 | 20 | , |
| 6 | 20 | , |
| 7 | 15 | , |
| 8 | 10 | , |
| 9 | 15 | , |
Exemplul 1
keidei.in
1 8 5
1 2
1 3
1 4
2 5
2 6
3 7
5 8
keidei.out
2 5 6 8
Explicație
Pentru primul exemplu: Pentru că putem să considerăm fiii oricărui nod din arbore în ce ordine dorim, putem să presupunem că parcurgerea noastră în adâncime parcurge fiii unui nod de la stânga la dreapta după ce stabilim ordinea.
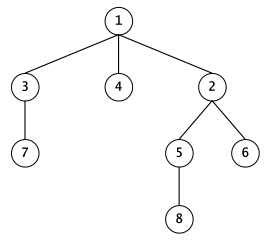 Figura 1: Dacă rearanjăm arborele primit ca să arate ca în figura de mai sus, parcurgerea va produce următorul rezultat: .
Figura 1: Dacă rearanjăm arborele primit ca să arate ca în figura de mai sus, parcurgerea va produce următorul rezultat: .
 Figura 2: Aici, parcurgerea va fi .
Figura 2: Aici, parcurgerea va fi .
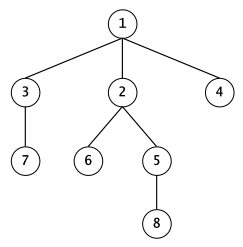 Figura 3: Aici, parcurgerea va fi .
Figura 3: Aici, parcurgerea va fi .
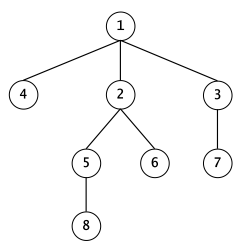 Figura 4: Aici, parcurgerea va fi .
Figura 4: Aici, parcurgerea va fi .
Putem verifica orice alt aranjament pentru a garanta că orice alt nod în afară de nu poate fi pe a -a poziție într-o parcurgere în adâncime pre-ordine.
Exemplul 2
keidei.in
1 17 15
1 2
1 3
1 4
2 5
3 6
3 7
4 8
5 9
5 10
8 11
8 12
8 13
8 14
9 15
10 16
10 17
keidei.out
3 10 11 12 13 14 16 17
Exemplul 3
keidei.in
2 8 5
1 2
1 3
2 4
2 5
2 7
2 8
3 6
keidei.out
4 5 7 8
Explicație
Pentru al treilea exemplu, putem observa că oricum am aranja arborele, primele noduri din parcurgere vor fi ori , ori . Dacă este înaintea lui în parcurgere, atunci va fi neapărat ultimul nod din parcurgere. Dacă ar fi înaintea lui , atunci va fi neapărat pe a patra poziție în parcurgere. Astfel, singurele noduri care pot fi pe a -a poziție sunt .