Se dă un graf conex neorientat $G$ cu $N$ noduri și $M$ muchii, fiecare muchie având asociat un cost.
Un arbore parțial pentru $G$ este un subgraf cu structura de arbore, care cuprinde toate nodurile și o parte din muchii.

Cerință

Se cere găsirea unui arbore parțial al grafului $G$, astfel încât diferența dintre cel mai mare și cel mai mic cost al unei muchii să fie minimă.

Date de intrare

Fisierul de intrare va conține pe prima linie numerele $N$ și $M$, separate printr-un spațiu. Pe urmatoarele $M$ linii se vor găsi muchiile grafului sub forma X Y C, cu semnificația că există muchie neorientată între $X$ și $Y$ de cost $C$.

Date de ieșire

Fisierul de ieșire va contine pe prima linie diferența minimă dintre cel mai mare și cel mai mic cost al muchiilor unui arbore parțial din $G$.

Restricții și precizări

• $2 \leq N \leq 30 \ 000$;
• $1 \leq M \leq 100 \ 000$;
• $1 \leq X < Y \leq N$;
• $1 \leq C \leq 1 \ 000 \ 000 \ 000$;
• între oricare două noduri există cel mult o muchie;
• Pentru $20$ de puncte, $1 \leq M \leq 20$;
• Pentru $20$ de puncte, $2 \leq N \leq 100$ și $1 \leq M \leq 100$;
• Pentru $20$ de puncte, $2 \leq N \leq 1000$ și $1 \leq M \leq 10 \ 000$;
• Pentru $20$ de puncte, $M\cdot(M-N)\cdot (M-N) \leq 10^{7}$;
• Pentru $20$ de puncte, nu există restricții suplimentare.

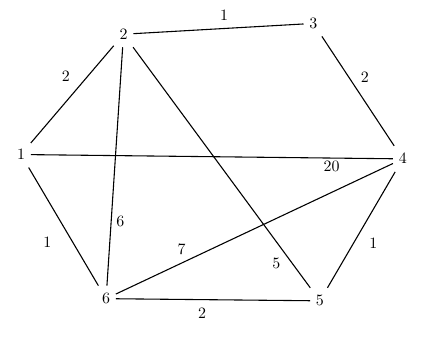
Exemplu

weightdif.in

6 10
1 2 2
2 3 1
3 4 2
4 5 1
5 6 2
1 6 1
1 4 20
2 5 5
2 6 6
4 6 7

weightdif.out

1

Explicație

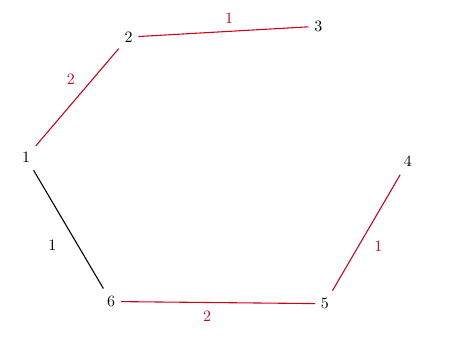
Graful din exemplu:

Un arbore parțial cu diferența minimă dintre costul maxim și cel minim de pe muchii: