retrotrees

Cerința

Se dă un graf neorientat conex cu $n$ noduri si $m$ muchii cu costuri. O colorare în alb și negru a grafului este corectă dacă:

• Subgraful obținut din nodurile albe și muchiile care conectează două noduri albe este conex;
• Subgraful obținut din nodurile negre și muchiile care conectează două noduri negre este conex;

Valoarea unei colorări corecte este egală cu suma costurilor muchiilor din arborii parțiali de cost minim ale celor două subgrafuri rezultate.

Care este valoarea minimă a unei colorări corecte a grafului dat?

Date de intrare

Pe prima linie a fișierului de intrare retrotrees.in se vor afla două numere $n$ și $m$ ($2 \le n \le 3 \cdot 10^5$, $1 \le m \le min(3 \cdot 10^5,\frac{n \cdot (n-1)}{2})$) — numărul de noduri, respectiv numărul de muchii ale grafului.

Pe fiecare dintre următoarele $m$ linii se vor afla trei numere $u$ și $v$ și $c$ ($1 \le u,v \le n$, $u \neq v$, $1 \le c \le 10^9$), cu semnificația că există o muchie neorientată între nodurile $u$ și $v$ cu costul $c$.

Se garantează că pentru orice pereche de noduri $(u,v)$, există cel mult o muchie între $u$ și $v$.

Date de ieșire

Fișierul de ieșire retrotrees.out va conține valoarea minimă a unei colorări corecte a grafului dat.

Restricții

• Pentru $15$ puncte, $m=n-1$
• Pentru $25$ de puncte, $n \le 15$
• Pentru $25$ de puncte, $n,m \le 3000$
• Pentru $35$ de puncte, nu se impun restricții suplimentare.

Exemple

Exemplu 1:

retrotrees.in

4 5
1 2 4
2 3 1
2 4 2
1 3 3
3 4 3

retrotrees.out

3

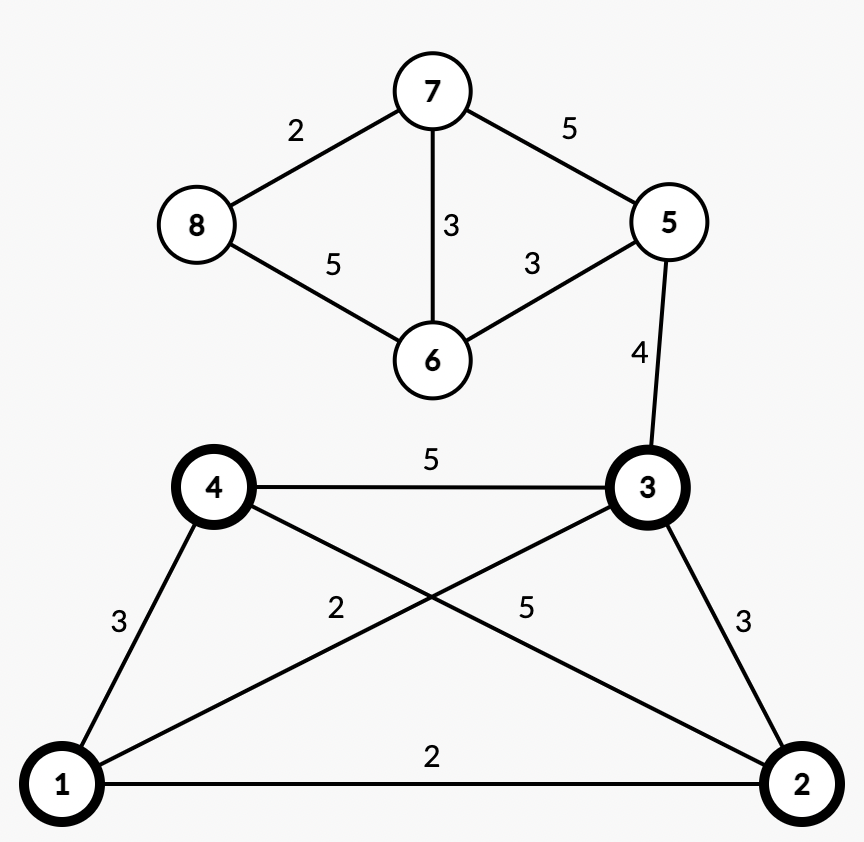
Exemplu 2:

retrotrees.in

8 12
1 2 2
1 3 2
1 4 3
2 3 3
2 4 5
3 4 5
3 5 4
5 6 3
5 7 5
7 8 2
6 7 3
6 8 5

retrotrees.out

15

Exemplu 3:

retrotrees.in

15 15
4 1 5
4 2 7
2 6 13
6 11 7
11 13 9
4 12 11
14 6 5
15 14 15
13 8 10
5 2 10
11 10 13
3 10 14
7 5 14
9 4 12
6 5 8

retrotrees.out

125

Explicații

O colorare corectă optimă a grafului din primul exemplu

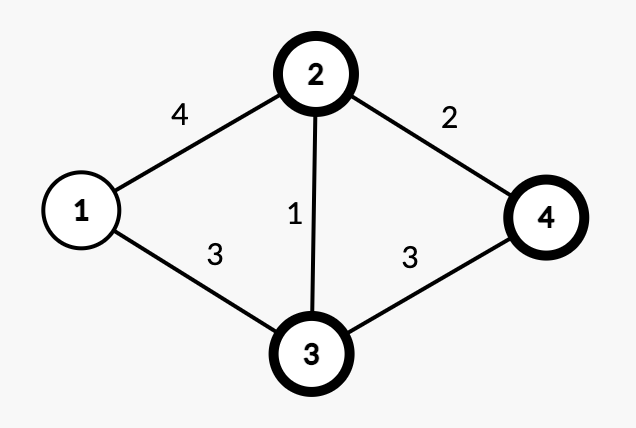
Graful parțial format din nodurile albe conține nodul $1$ și nicio muchie, prin urmare arborele parțial de cost minim alb va avea costul total egal cu $0$.

Graful parțial format din nodurile negre conține nodurile $2,3,4$ și muchiile $(2,3)$, $(2,4)$ și $(3,4)$. Arborele parțial de cost minim obținut din subgraful negru va conține muchiile $(2,3)$ și $(2,4)$, cu un cost total de $1+2=3$.

O colorare corectă optimă a grafului din al doilea exemplu