Wildcards

Numim pattern un șir nevid format doar din caracterele 0, 1 și ?. Spunem că două patternuri A și B de aceeași lungime se potrivesc dacă și numai dacă caracterele ? pot fi înlocuite convenabil cu 0 și 1 astfel încât cele două șiruri să devină identice. De exemplu, pentru A = 110?1, B = 1?001, C = ??1?1, șirurile A și B se potrivesc (se poate forma șirul 11001 prin înlocuirea semnelor de întrebare cu valori), dar șirurile A și C nu se potrivesc.

Se dă un arbore (graf neorientat conex aciclic) cu N noduri. Se cere să se atribuie fiecărui nod câte un șir format din caracterele 0, 1 și ? (un pattern) astfel încât să se respecte următoarele proprietăți:

• Toate patternurile să aibă aceeași lungime, care să fie cât mai mică (a se vedea rubrica Punctare).
• Pentru oricare două noduri distincte u și v, patternurile asociate acestora se potrivesc dacă și numai dacă există muchia (u, v) în arbore.

Detalii de implementare

Veți implementa funcția cu următorul antet:

std::vector<std::string> patterns(std::vector<std::pair<int, int>> edges)

Funcția patterns va fi apelată exact o dată în cadrul unui test. Vectorul edges va avea dimensiune N - 1 și va reprezenta muchiile neorientate ale arborelui date ca perechi de noduri adiacente. Formal, $edges_i$ este egal cu o pereche $(u_i, v_i) (0 \le i < N - 1, 1 \le u_i, v_i \le N)$, cu semnificația că există o muchie neorientată între nodurile $u_i$ și $v_i$. Nodurile sunt indexate de la 1. Se garantează că muchiile vor forma un graf conex aciclic.

Funcția trebuie să returneze un vector care să conțină exact N patternuri nevide de aceeași lungime, formate doar din caracterele 0, 1 și ? (nu obligatoriu toate trei). Șirul de pe poziția i (0 ≤ i < N) va reprezenta patternul asociat nodului cu indicele i + 1.

Pentru ca soluția să fie validă, trebuie ca patternurile returnate să respecte condițiile menționate mai sus. În caz contrar, graderul va termina programul și va nota testul ca fiind incorect.

Punctare

Atenție! Această problemă este punctată parțial. Testele din cadrul fiecărui subtask vor avea asociată o lungime maximă $prag_{sup}$ acceptată. Orice răspuns returnat de funcția voastră care conține patternuri mai lungi decât această lungime va fi considerat un răspuns incorect pe acest test.

Există, de asemenea, și un prag de lungime $prag_{inf}$ care asigură punctajul maxim pe testul respectiv. Dacă funcția returnează o soluție mai bună decât pragul inferior de lungime, aceasta va primi punctajul maxim pe test. Dacă lungimea patternurilor returnate este între aceste două limite, punctajul primit va fi calculat după formula:
$\displaystyle punctaj = \left\lfloor \frac{1}{2} \cdot P_{subtask} \cdot \left(1 + \frac{prag_{sup}-ans+1}{prag_{sup}-prag_{inf}+1}\right) \right\rfloor$

Aici ans reprezintă lungimea patternurilor din răspunsul returnat de concurent, iar $P_{subtask}$ reprezintă punctajul alocat subtask-ului din care face parte respectivul test, iar $\lfloor x \rfloor$ reprezintă partea întreagă inferioară a numărului real x. A se observa că, pentru $ans = prag_{inf}$, se obține întreg punctajul testului, iar pentru $ans = prag_{sup}$, se obține jumătate din punctajul testului.

Punctajul total acordat unui subtask este egal cu minimul punctajelor acordate fiecărui test din cadrul subtask-ului.

Subtask 1 (6 puncte)

• 2 ≤ N ≤ 10
• $prag_{inf} = 100$
• $prag_{sup} = 100$

Subtask 2 (9 puncte)

• 2 ≤ N ≤ 100
• $prag_{inf} = 100$
• $prag_{sup} = 100$

Subtask 3 (5 puncte)

• 2 ≤ N ≤ 10 000
• $prag_{inf} = 34$
• $prag_{sup} = 34$
• Arborele este un lanț de $N$ noduri

Subtask 4 (6 puncte)

• 2 ≤ N ≤ 10 000
• $prag_{inf} = 34$
• $prag_{sup} = 34$
• Arborele este binar complet

Subtask 5 (42 puncte)

• 2 ≤ N ≤ 10 000
• $prag_{inf} = 101$
• $prag_{sup} = 200$

Subtask 6 (32 puncte)

• 2 ≤ N ≤ 10 000
• $prag_{inf} = 34$
• $prag_{sup} = 42$

Model de grader

Graderul va citi de la consolă datele de intrare în următorul format:

• linia 1: N
• linia 1 + i (1 ≤ i ≤ N - 1): $u_i \ v_i$ (separate prin spațiu), reprezentând muchia $(u_i, v_i)$

Graderul va afișa la consolă răspunsul vostru, în următorul format:

• linia i (1 ≤ i ≤ N): $p_i$, reprezentând patternul asociat nodului i

Exemple

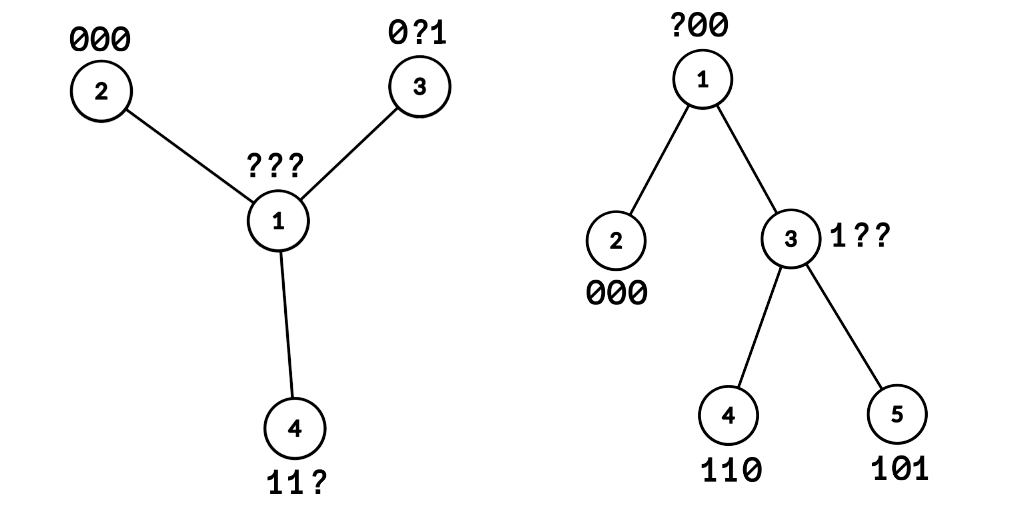
stdin

4	
1 2
1 3
1 4

stdout

???
000
0?1
11?

stdin

3
1 2
2 3

stdout

0
?
1

stdin

5
1 2
1 3
3 4
3 5

stdou

?00
000
1??
110
101

stidn

2
2 1

stdout

?
?

Explicație

Aceasta este figura pentru primul, respectiv cel de-al treilea exemplu: