mozaic

Rapunzel, plictisită de modul în care arată castelul ei, doreşte să facă nişte modificări. Astfel, ea a comandat un nou mozaic pentru a îl pune la intrare. Meşterii palatului, ştiind cât de nehotărâtă este prinţesa, au decis să vină cu cât mai multe modele posibile.

Mozaicul comandat este unul simplu, alcătuit din două benzi suprapuse de lungime $N$. Pentru a-l realiza, meşterii dispun de un număr infinit de plăcuţe dreptunghiulare cu lungimi variabile si lăţimi egale cu lăţimea unei benzi. Oricare două plăcuţe de lungimi diferite au şi modele diferite.

Pentru a nu încărca prea mult mozaicul, o bandă o să conţină acelaşi model de plăcuţă. Deoarece materialele sunt scumpe, meşterii doresc să folosească integral fiecare plăcuţă, fără sa depăseaşcă lungimea mozaicului.

În timp ce lucrau la mozaic, prinţul Flynn a venit şi el cu o condiţie: numărul de plăcuţe pe care îl folosesc pentru prima bandă şi numărul de plăcuţe pentru a doua bandă să fie prime între ele.

Speriaţi puţin de această condiţie, meşterii vă cer ajutorul pentru a calcula câte modele o să aducă în faţa prinţesei, la terminarea comenzii.

Cerința 1

Înainte să se apuce de treabă, meşterii doresc să ştie lungimea plăcuţelor ce ar putea fi utilizate în crearea mozaicului.

Cerința 2

Să se determine numărul de modele pe care prinţesa o să le primească de la meşteri.

Date de intrare

Pe prima linie se găseşte un număr $T$ care poate să fie $1$ sau $2$, în funcţie de numărul task-ului care urmează a fi realizat. Pe următoarea linie se găseşte un număr $N$, care reprezintă lungimea mozaicului.

Date de ieșire

Pentru $T = 1$ în fişierul de ieşire o să se afişeze, separate printr-un spaţiu, toate lungimile plăcuţelor, în ordine crescătoare.

Pentru $T = 2$, în fişierul de ieşire o să se afişeze numărul de modele.

Restricții și precizări

• Plăcuţele au orice lungime număr natural nenul;
• Există un număr infinit de plăcuţe de aceaşi lungime;
• $1 \leq T \leq 2$;
• $q \leq N \leq 2 \ 000 \ 000$;
• Pentru $20$ de puncte, $T = 1$;
• Pentru $30$ de puncte, $T = 2$ și $1 \leq N \leq 500$;
• Pentru $10$ puncte, $T = 2$, $N \gt 500$ și $N$ este prim;
• Pentru $40$ de puncte, $T = 2$.

Exemplul 1

stdin

1
9

stdout

1 3 9

Explicație

O banda de lungime $9$ se poate completa cu $9$ plăcuţe de lungime $1$, $3$ plăcuţe de lungime $3$ sau o plăcuţă de lungime $9$.

Exemplul 2

stdin

2
9

stdout

3

Explicație

cele trei modele pe care prinţesa le poate realiza conţin plăcuţele cu următoarele lungimi:

$1 \ 9$
$3 \ 9$
$9 \ 9$

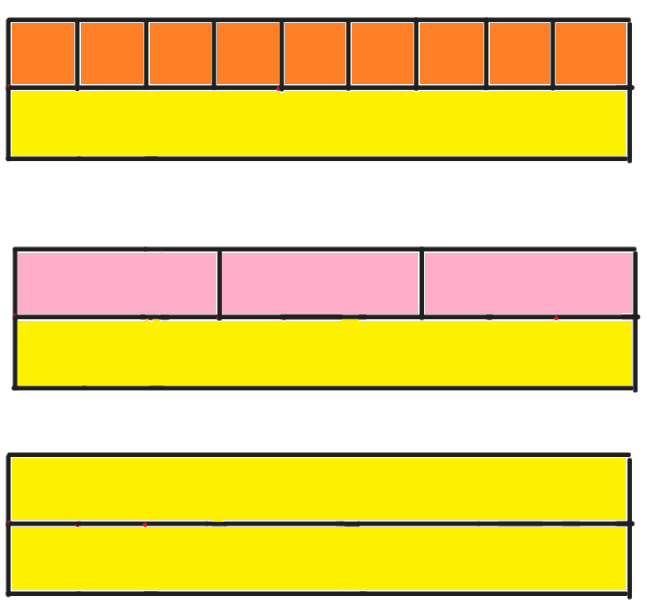
Se poate observa ca $1 \ 3$ nu este un model valid, întrucât numărul de plăcuţe necesare pentru a completa prima bandă ar fi $9$, iar numarul de plăcuţe necesare pentru a completa a doua bandă ar fi $3$, cele două numere nefiind prime între ele.

De asemenea, nu au fost luate in calcul modelele $9 \ 1$ şi $9 \ 3$, fiind considerate aceleaşi cu modelele $1 \ 9$, respectiv $3 \ 9$.

Exemplul 3

stdin

2
17

stdout

2

Explicație

Cele două modele pe care prinţesa le poate realiza conţin plăcuţele cu următoarele lungimi:

$1 \ 17$
$17 \ 17$