„L'essentiel est invisible pour les yeux.”
Fie un graf neorientat conex cu noduri și muchii. Nodurile sunt numerotate de la la iar muchiile au asociate costuri numere naturale date.
Un graf parţial al lui conex şi fără cicluri este denumit arbore parţial. Costul unui arbore parțial este suma costurilor muchiilor arborelui. Deoarece unele muchii pot avea același cost, este posibil ca graful să aibă mai mulți arbori parțiali de cost minim.
Definim o muchie a grafului ca fiind esențială dacă ea face parte din toți arborii parțiali de cost minim ai lui .
Cerință
Scrieţi un program care, cunoscând graful, rezolvă următoarele două cerinţe:
- determină costul unui arbore parțial de cost minim al lui ;
- determină numărul de muchii esențiale ale grafului .
Date de intrare
Fişierul de intrare esentiale.in conţine pe prima linie numerele naturale , și , reprezentând numărul de noduri, numărul de muchii și numărul cerinței ( sau ). Următoarele linii conțin câte trei numere: , , , cu semnificația că între nodurile și există o muchie având costul .
Date de ieșire
Fișierul de ieșire esentiale.out va conţine o singură linie pe care va fi scris răspunsul la cerinţa .
Restricții și precizări
- , pentru orice muchie din
- Între oricare două noduri există cel mult o muchie.
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 34 | |
| 2 | 29 | și |
| 3 | 27 | și |
Exemplul 1
esentiale.in
5 7 1
1 2 3
3 2 4
3 4 3
1 3 2
2 5 3
5 4 1
4 1 4
esentiale.out
9
Explicație
, deci se rezolvă doar prima cerință.
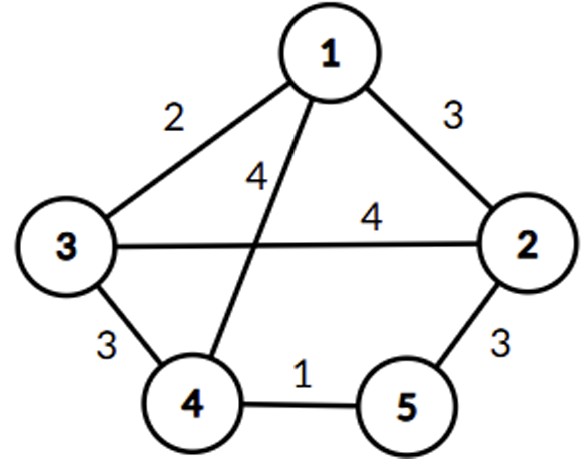
Graful este cel din desen și unul din arborii parțiali de cost minim ai lui este format din muchiile: , , , . Costul total minim este , egal cu suma costurilor muchiilor în ordinea specificată mai sus.
Exemplul 2
esentiale.in
5 7 2
1 2 3
3 2 4
3 4 3
1 3 2
2 5 3
5 4 1
4 1 4
esentiale.out
2
Explicație
, deci avem de rezolvat cerința a doua, pentru același graf .
Există trei arbori parțiali de cost minim, formați din următoarele muchii:
- , , ,
- , , ,
- , , ,
Doar două muchii sunt în toți arborii parțiali de cost minim și anume și .