dag

Un graf aciclic orientat (DAG - Directed Acyclic Graph) este un graf orientat fără cicluri.

Fie G un graf orientat aciclic simplu (adică nu conține muchii multiple între aceleaşi noduri sau muchii de la un nod la el însuşi) în care nodurile sunt etichetate cu primele N numere naturale.

O sortare topologică a nodurilor unui graf aciclic orientat G este o ordonare a nodurilor astfel încât, dacă există un arc (i, j) ∈ G, atunci i apare înaintea lui j în această ordonare. O astfel de ordonare se poate reprezenta ca o permutare P a etichetelor nodurilor grafului G.

Dintre toate sortările topologice ale unui graf, numim sortarea topologică minimă lexicografic acea sortare topologică a cărei permutare este mai mică lexicografic decât permutarea oricărei alte sortări topologice.

O permutare $a_1, a_2, ..., a_N$ este mai mică lexicografic decât o altă permutare $b_1, b_2, ..., b_N$ dacă există un număr întreg S mai mic sau egal cu N astfel încât: $a_1 = b_1, a_2 = b_2, ..., a_{S–1} = b_{S–1}$, iar $a_S < b_S$.

Cerință

Se dă o permutare P de lungime N. Câte grafuri orientate aciclice etichetate cu primele N numere naturale au proprietatea că P este sortarea lor topologică minimă lexicografic?

Date de intrare

În fișierul dag.in se află pe prima linie numărul N. Pe a doua linie se vor afla N numere distincte cu valori între 1 și N reprezentând permutarea P.

Date de ieșire

În fișierul dag.out trebuie să se găsească un singur număr care reprezintă numărul de grafuri orientate aciclice de N noduri pentru care P este sortarea lor topologică minimă lexicografic. Deoarece această valoare poate fi foarte mare, se cere să afișați doar restul modulo 1 000 000 007 al acesteia.

Restricții

• 2 ≤ N ≤ 200 000;
• Pentru teste în valoare de 10 puncte, N ≤ 6;
• Pentru alte teste în valoare de 55 puncte, N ≤ 2 500.

Exemplul 1

dag.in

3
3 1 2

dag.out

3

Explicație

În primul exemplu există 3 grafuri orientate aciclice simple cu 3 noduri a căror sortare topologică minimă este $P_1 = 3$, $P_2 = 1$, $P_3 = 2$.

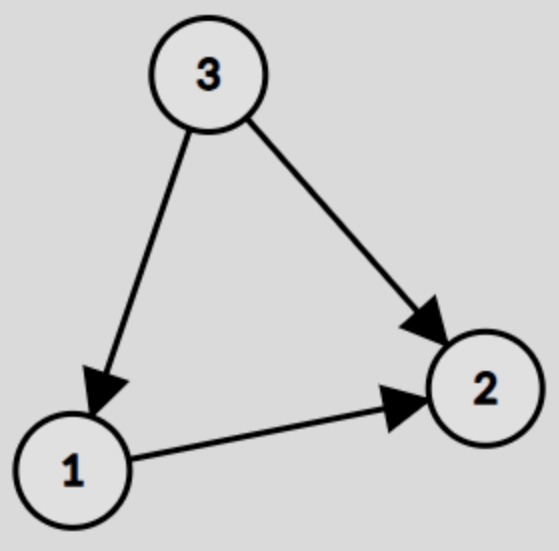
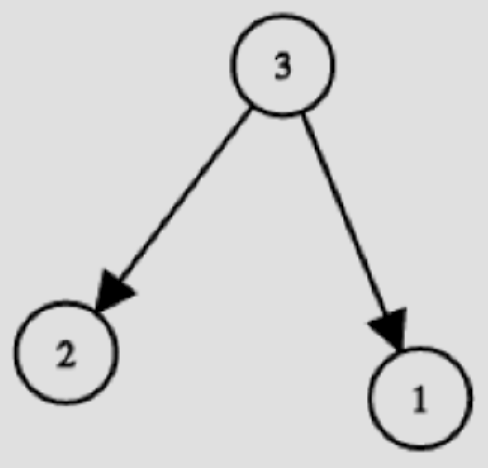
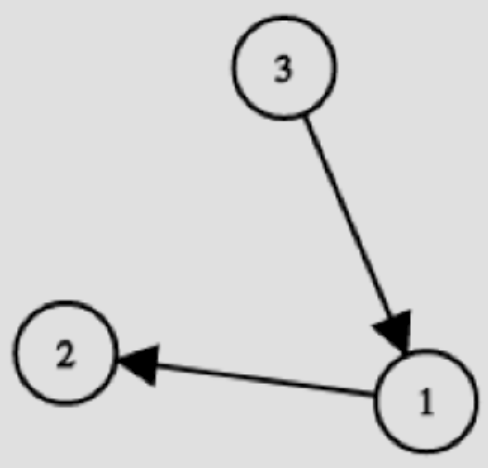
Exemplul 2

dag.in

10
1 2 3 5 4 6 7 8 10 9

dag.out

92960636