suma

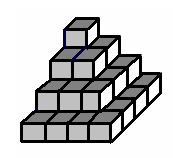
Constructorii angajaţi de faraonul Keops au terminat construirea piramidei în trepte mult visată. Măreaţa piramidă are $n$ camere identice de formă cubică, numerotate de la $1$ la $n$, dispuse pe $m$ niveluri astfel:

• camera din vârful piramidei formează nivelul $1$ şi are numărul $1$;
• nivelul $2$ al piramidei este format din următoarele $4$ camere care în secţiune cu un plan paralel cu baza au aspectul unei matrice cu $2$ linii şi $2$ coloane; camerele de pe nivelul $2$ sunt numerotate de la $2$ la $5$ în ordinea crescătoare a liniilor matricei, iar pe aceeaşi linie în ordinea crescătoare a coloanelor matricei;
  ...
• nivelul $m$ al piramidei este format din $m \times m$ camere şi au, în secţiune cu un plan paralel cu baza, aspectul unei matrice cu $m$ linii şi $m$ coloane; camerele de pe nivelul $m$ sunt numerotate în continuarea celor de pe nivelurile $1, 2, ..., m - 1$, în ordinea crescătoare a liniilor matricei de secţiune, iar pe aceeaşi linie în ordinea crescătoare a coloanelor matricei. De exemplu, piramida din desenul de mai sus are $n = 30, m = 4$ iar camerele sunt numerotate şi dispuse pe niveluri astfel:
  
  
  
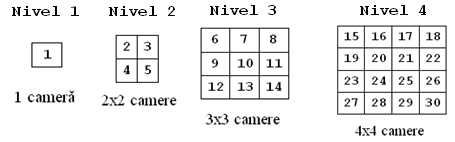
  Nivelurile de camere sunt poziţionate astfel încât camerele de pe prima linie şi prima coloană a fiecărui nivel să se suprapună. Pentru exemplul dat, camerele $1, 2, 6$ şi $15$ sunt situate una sub alta, în această ordine.

Accesul în oricare din camerele piramidei, situate pe diferite niveluri, se realizează prin drumuri construite astfel:

• intrarea în piramidă se face doar prin camera din vârful ei, cea cu numărul $1$;
• din camera cu numărul $k$ de pe un drum se poate intra într-una din cele patru camere situate pe nivelul imediat următor al piramidei şi anume: camera situată sub cea cu numărul $k$ sau una din cele trei camere vecine acesteia în secţiune (în direcţiile Est, Sud-Est, Sud, considerând secţiunile poziţionate ca în imaginile de mai sus). De exemplu, din camera cu numărul $10$ se poate intra într-una din camerele cu numerele: $20, 21, 24$ sau $25$.

Faraonul priveşte cu mândrie şi tristeţe la frumoasa piramidă. Banii din visterie s-au împuţinat iar camerele piramidei trebuie finisate şi decorate. Scribul său favorit a refăcut toate calculele, a eliminat obiectele inutile şi a stabilit pentru fiecare cameră $k$ un cost $c_k$ aferent finisării şi decorării ei ($1 ≤ k ≤ n$).

Însă, suma totală necesară fiind încă mare, faraonul i-a cerut scribului să aleagă un drum, dintre cele construite, care să treacă prin toate nivelurile piramidei astfel încât suma s a tuturor costurilor aferente finisării şi decorării camerelor de pe acest drum să fie minimă. Deocamdată, doar aceste camere vor fi aranjate...

Cerinţă

Scrieţi un program care să determine numărul $m$ de niveluri ale piramidei, suma minimă $s$ a tuturor costurilor aferente finisării şi decorării camerelor de pe un drum ce trece prin toate nivelurile piramidei, construit în modul descris în enunţ, precum şi un astfel de drum pentru care se obţine suma minimă, putând fi ales de scrib.

Date de intrare

Fişierul de intrare suma.in conţine pe prima linie numărul natural nenul $n$ reprezentând numărul de camere din piramidă. A doua linie conţine $n$ numere naturale nenule $c_1, c_2,…, c_n$, separate prin câte un spaţiu, reprezentând costurile aferente finisării şi decorării camerelor, în ordinea numerotării lor.

Date de ieşire

Fişierul de ieşire suma.out va conţine pe prima linie două numere naturale $m$ şi $s$, separate printr-un singur spaţiu, cu semnificaţia din enunţ. Cea de-a doua linie va conţine, separate prin câte un spaţiu, în ordinea parcurgerii lor, numerele camerelor de pe un drum ce trece prin toate nivelurile piramidei, drum pentru care se obţine suma minimă $s$.

Restricţii şi precizări

• $1 ≤ n ≤ 63\ 365$
• Pentru fiecare valoare $n$ citită se poate construi în modul descris în enunţ o piramidă în trepte cu $n$ camere
• $1 ≤ c_1, c_2, ..., c_n < 100$
• Dacă există mai multe drumuri ce trec prin toate nivelurile piramidei şi pentru care se obţine suma minimă $s$, atunci drumul ales va fi cel mai mic drum din punct de vedere lexicografic.
• Drumul $a_1, a_2, a_3, …, a_m$ este mai mic, din punct de vedere lexicografic, ca drumul $b_1, b_2, b_3, …, b_m$ dacă există un indice $j$ ($1 ≤ j ≤ m$) astfel încât $a_1=b_1, a_2=b_2 ,….,a_{j-1}=b_{j-1}$ şi $a_j < b_j$.
• Se acordă:
• $10$ din punctaj pentru determinarea corectă a numărului $m$ de niveluri ale piramidei
• $30$ din punctaj pentru determinarea corectă a sumei minime $s$
• $60$ din punctaj pentru determinarea corectă a drumului cerut.

Exemplu

suma.in

14
7 8 4 5 5 8 4 2 7 7 8 3 1 6

suma.out

3 13
1 3 8

Explicații

Piramida conţine $14$ camere dispuse pe $m = 3$ trei niveluri. Nivelurile conţin valorile:



Suma minimă $s$ a tuturor costurilor aferente finisării şi decorării camerelor de un drum ce trece prin toate cele $3$ niveluri ale piramidei este $13$. Există mai multe drumuri pentru care se poate obţine suma minimă: $[1,3,8], [1,4,13], [1,5,13]$. Din punct de vedere lexicografic, cel mai mic drum dintre aceste drumuri este: $[1,3,8]$.