Holes and Balls

There are $2 \cdot N + 1$ consecutive positions in a line, indexed from $0$ to $2\cdot N$ from left to right.

• There are $N$ balls, initially placed at positions $1, 3, 5, \ldots, 2 \cdot N - 1$.
• There are $N + 1$ holes, located at positions $0, 2, 4, \ldots, 2 \cdot N$.

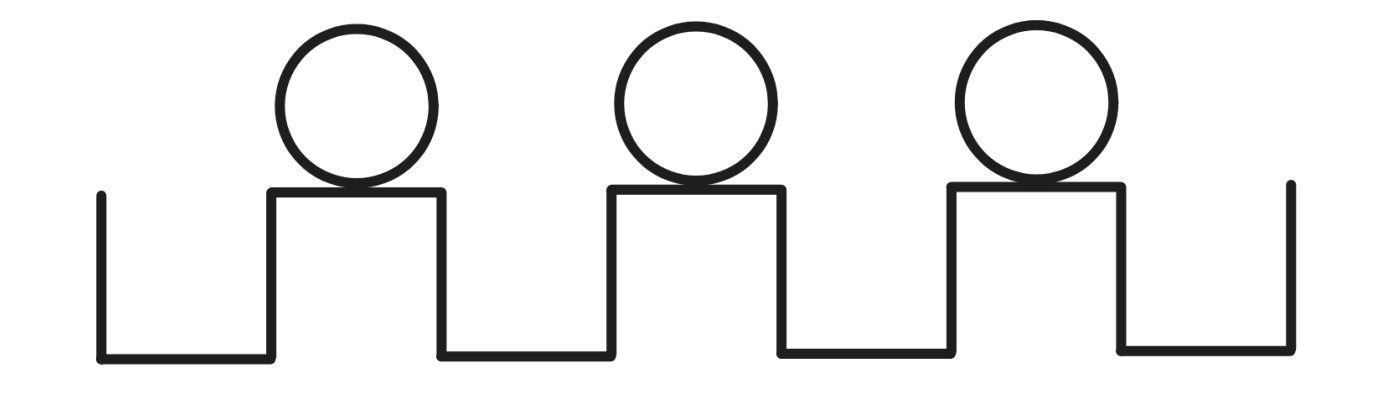
You have to perform exactly $N$ moves, one for each ball. In a single move:

• Choose any unused ball.
• Push it either left or right.
• The ball will continue moving in that direction until it reaches the first empty hole, where it will fall in and stop.

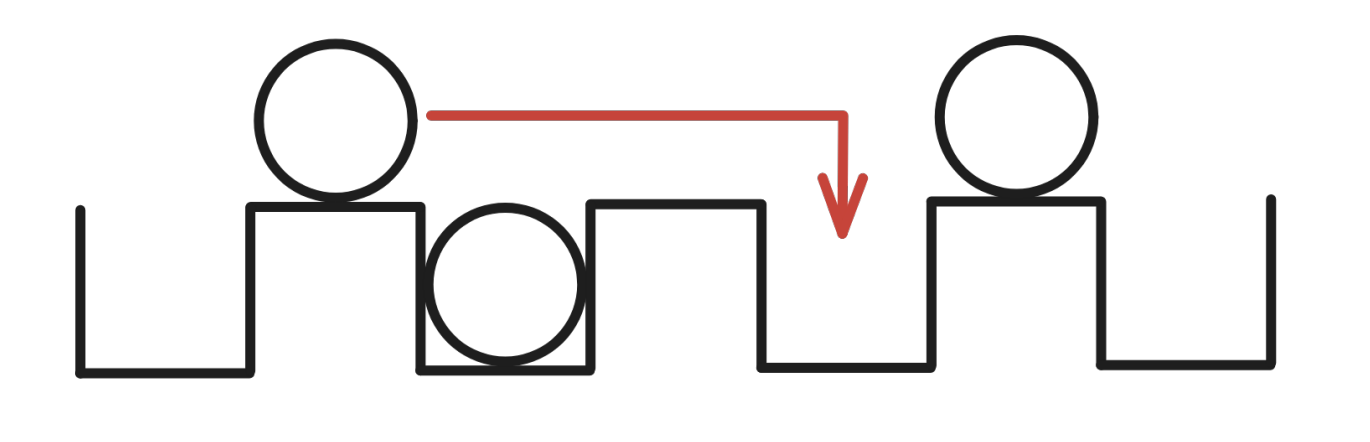
Note that there are $N! \cdot 2^{N}$ distinct valid sequences of moves (each permutation of the balls, with each ball pushed either left or right), and at the end of every valid sequence exactly one hole will remain empty.

Your task is to compute, for each hole position $i$ from $0$ to $2N$, how many of these sequences leave hole $i$ empty at the end.

Since the answers may be large, calculate them modulo a given prime $M$.

Input data

The first and only line of the input consists of two space-separated integers $N$ and $M$ - the number of balls and the prime modulus, respectively.

Output data

Output a single line containing $N + 1$ space-separated integers - the number of different sequences of moves that leave hole $i$ (the hole at position $2\cdot i$ for each $i$ from $0$ to $N$) empty.

Constraints and clarifications

• $1 \le N \le 1 \ 000 \ 000$.
• $100 \ 000 \ 000 \le M \le 1 \ 000 \ 000 \ 007$.
• $M$ is prime.

Example 1

stdin

3 1000000007 

stdout

15 9 9 15

Example 2

stdin

7 100000007 

stdout

135135 72765 59535 55125 55125 59535 72765 135135