
Everything seems a bit odd these days! To embrace the oddness, we present you an odd challenge!.
You are given an undirected graph with vertices and edges. The graph is not necessarily connected.
Your task is to construct a spanning subgraph of such that the number of vertices with odd degree in is maximized.
Write a program that selects a subset of edges from (possibly all or none) to delete, such that the resulting graph spans all vertices and has the maximum possible number of vertices with odd degree.
Input data
The first line of the input contains and , the number of vertices and the number of edges in .
The next lines each contain a pair of integers , describing the edges in the graph.
Output data
The first line of the output contains two integers:
- , the maximum number of vertices with an odd degree in a spanning subgraph .
- : the number of edges to be deleted from to obtain .
The next lines each contain a pair of integers: the endpoints of an edge (in arbitrary order) which you choose to delete.
If there are multiple solutions, you may print any correct one.
Constraints and clarifications
- .
- .
- and for each .
- There is at most one edge between any pair of vertices.
- A spanning subgraph of is a subgraph that includes all vertices of but may include only a subset of the edges. The resulting subgraph can have cycles, multiple components, or isolated vertices.
| # | Score | Restrictions |
|---|---|---|
| 0 | 0 | Examples |
| 1 | 7 | . |
| 2 | 12 | . |
| 3 | 14 | The graph is a simple cycle. |
| 4 | 16 | The graph is a tree. |
| 5 | 51 | No additional limitations. |
Example 1
stdin
4 3
1 2
2 4
4 1
stdout
2
1
4 2
Explanation
In the first sample case, the graph in the input is shown in the figure below.
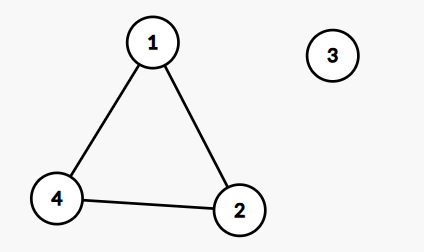
The maximum number of odd vertices in a spanning subgraph is . We can remove any edge, or any pair of two edges to obtain such a subgraph.
Example 2
stdin
6 9
1 2
2 3
3 1
1 4
2 5
3 6
4 5
5 6
6 4
stdout
6
6
1 2
2 3
3 1
4 5
5 6
6 4