Bob has just started exploring the fascinating world of mathematics.
One day, his teacher introduced him to the multiplication table - an infinite grid where the value at row and column (for all integers ) is simply .
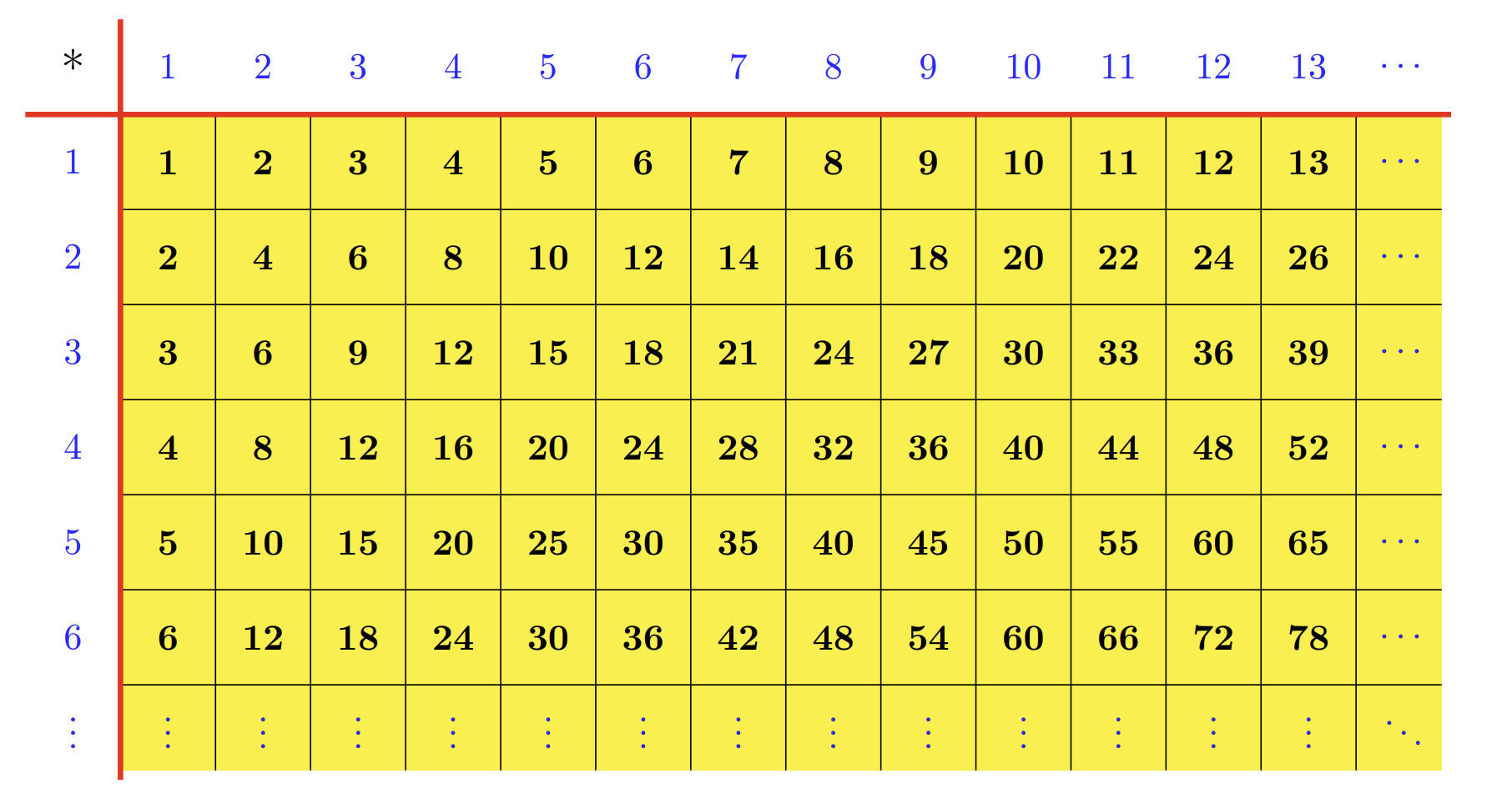
Bob was fascinated and began practicing with a small section of the table.
However, while Bob was taking a break, his mischievous friend scribbled over Bob's worksheet, replacing some of the numbers with either incorrect values or question marks (?).
Formally, he is left with a table of rows and columns, where each cell contains either:
- A positive integer, or
- A question mark (
?) indicating an unknown or erased value.
Now Bob isn't sure if what he has is still a valid piece of the multiplication table. Can you help Bob figure it out?
Your task is to determine whether it's possible to replace the question marks with positive integers such that the entire table corresponds to a valid subrectangle
of the infinite multiplication table.
You do not need to find the missing numbers - just decide whether such a valid completion exists.
Input data
The first line contains the integers , , representing the number of rows and columns in Bob's table.
This is followed by lines, where line () represents row of Bob's table (),
consisting of question marks and integers.
Output data
- Print
YESif the table can be a part of the multiplication table after filling in the question marks. - Print
NOif it is impossible.
Constraints and clarifications
- .
-
?or for each , .
| # | Score | Restrictions |
|---|---|---|
| 0 | 0 | Examples |
| 1 | 12 | , , and the table contains no ? |
| 2 | 11 | , ? or . |
| 3 | 26 | , ? or . |
| 4 | 51 | No additional limitations. |
Example 1
stdin
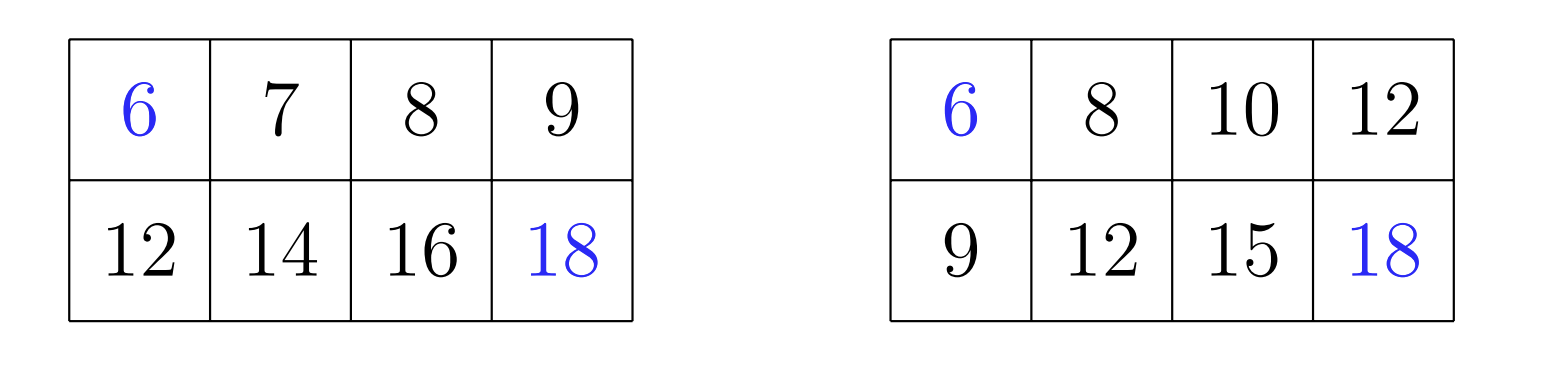
2 4
6 ? ? ?
? ? ? 18
stdout
YES
Explanation
In the first sample case the answer is YES.
Please note that this does not mean, that we can identify the part of the multiplication table. Here we have two possibilities.
Example 2
stdin
2 2
? ?
? 3
stdout
NO
Explanation
In the second sample case either the first row or the first column is outside the multiplication table, as the number
only appears in the first row or the first column of the infinite grid.
Example 3
stdin
2 1
999997000002
999998000001
stdout
YES