Se dau două circuite, fiecare cu câte compartimente numerotate de la la , în sens orar pe circuitul roșu (stâng) și în sens antiorar pe circuitul albastru (drept). dintre aceste compartimente sunt comune celor două circuite, și anume compartimentele .
Circuitele conțin bile numerotate de la la . Inițial,
- Bilele se află în compartimentele de pe circuitul roșu.
- Bilele se află în compartimentele de pe circuitul albastru, sărind peste compartimentele comune.
Putem efectua două tipuri de mutări: Mutarea R rotește circuitul roșu în sens orar cu un compartiment, iar mutarea A rotește circuitul albastru în sens antiorar cu un compartiment.
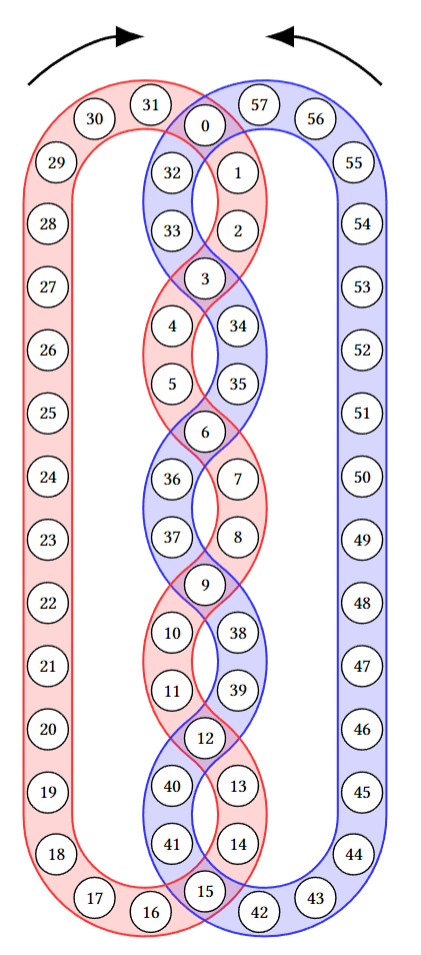
Figura arată circuitele pentru , și . O mutare R ar pune bila 0 în locul bilei 1, bila 1 în locul bilei 2, , bila 31 în locul bilei 0. O mutare A ar pune bila 0 în locul bilei 32, bila 32 în locul bilei 33, bila 33 în locul bilei 3, , bila 57 în locul bilei 0.
Dacă notăm cu valorile bilelor din compartimentele ale unui circuit, atunci codificarea circuitului este valoarea
Cerință
Date fiind , , , și o secvență de mutări R sau A, tipăriți codificările celor două circuite după efectuarea mutărilor.
Date de intrare
Pe prima linie se află întregii , , și . A doua linie conține caractere R sau A, fără spații.
Date de ieșire
Afișați două linii, prima conținând codificarea finală a circuitului roșu, iar a doua codificarea finală a circuitului albastru.
Restricții
- este par
| # | Scor | Restricții |
|---|---|---|
| 1 | 5 | |
| 2 | 7 | |
| 3 | 19 | Există cel mult mutări R. |
| 4 | 42 | |
| 5 | 27 | Fără alte restricții. |
Exemple
stdin
7 2 3 4
RRAA
stdout
74
133
stdin
32 6 3 2
RA
stdin
11195
21666
Explicație
În primul exemplu, circuitele evoluează astfel:
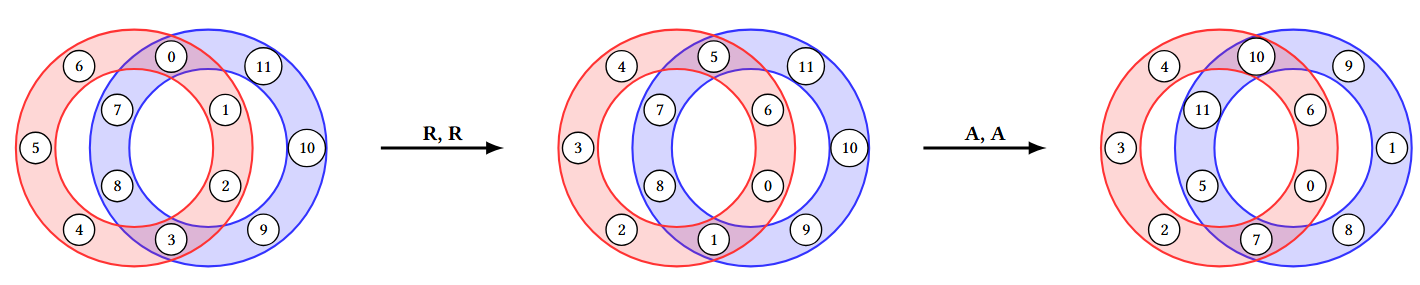
Codificarea finală a circuitului roșu este , iar codificarea circuitului albastru este .
Al doilea exemplu descrie circuitele de pe pagina 1. La final, conținutul circuitului roșu este:
57 0 1 33 3 4 35 6 7 37 9 10 39 12 13 41 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30,
iar conținutul circuitului albastru este:
57 31 32 33 2 34 35 5 36 37 8 38 39 11 40 41 14 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56.