Se dă o matrice cu linii și coloane în care unele celule sunt libere și altele sunt blocate. Scopul nostru este să plecam din colțul stânga sus al matricei și să ajungem în colțul dreapta jos astfel încât să trecem doar prin celule libere și mergând doar în jos sau la dreapta la fiecare pas.
Pentru a putea ajunge până în colțul dreapta-jos al matricei avem voie să facem următoarea operație de oricâte ori: alegem o linie a matricei și o transpunem la stânga sau la dreapta cu o celulă. Celulele noi apărute prin acest proces vor fi automat blocate.
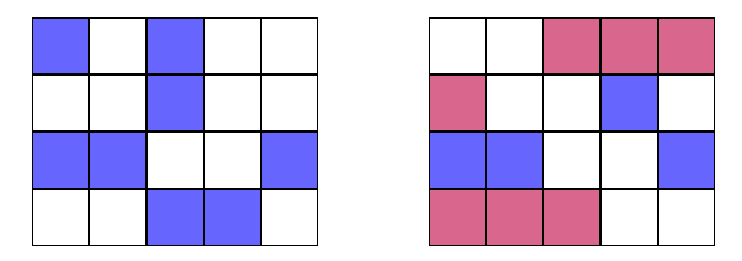
În următoarele imagini puteți vedea ce s-ar întâmpla dacă am aplica de ori operația de transpunere a primei linii la stânga:

În următoarele imagini puteți vedea ce s-ar întâmpla dacă am aplica de ori operația de transpunere a celei de-a treia linii la dreapta:

Cerință
Se cere să se calculeze numărul minim de operații prin care să se facă posibilă ajungerea din colțul stânga sus al matricei în colțul dreapta jos al matricei.
Date de intrare
Intrarea conține pe prima linie două numere naturale și .
Următoarele linii vor conține fiecare câte un șir binar de lungime , valorile de reprezentând celule blocate iar valorile de reprezentând celule libere.
Date de ieșire
Prima linie a ieșirii va conține un singur număr natural reprezentând numărul minim de operații necesar rezolvării problemei. Dacă ne este imposibil să ajungem din în se va afișa .
Restricții și precizări
- .
- .
| # | Scor | Restricții |
|---|---|---|
| 1 | 14 | |
| 2 | 21 | |
| 3 | 8 | |
| 4 | 57 | Fără restricții adiționale. |
Exemplul
stdin
4 5
10100
00100
11001
00110
stdout
7
Explicație
Transpunem prima linie la stânga de ori.
Transpunem a doua linie la dreapta o dată.
Transpunem a patra linie la dreapta de ori.
În total avem operații.