Task
Builder Bob is designing a new residential area in the city of Lazy Links. The area consists of houses, numbered from 1 to . The bidirectional streets between houses are built as follows:
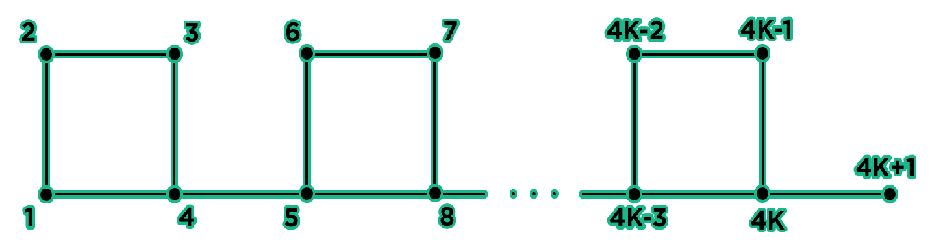
- For each integer such that , there is a street between house and house .
- For each integer such that , there is a street between house and house .
Bob envisions an ideal scenario where each player loots exactly two houses connected by a street. Each house can be looted by at most one player.
In how many different ways can the maximum number of players each loot two adjacent houses, such that no house is used more than once? Two ways are considered different if there is at least one pair of houses chosen in one arrangement and not in the other.
In other words, the question is: what is the number of maximum matchings that can be obtained?
Since the answer can be very large, output the result modulo .
Input data
The first line contains a single integer — the number of test cases.
Each of the next lines contains one integer — the number of houses in that test case.
Output data
For each test case, output a single integer — the number of distinct ways to select disjoint pairs of adjacent houses for the maximum number of players.
Example
stdin
3
8
3
127205
stdout
4
2
20761964
Explanation
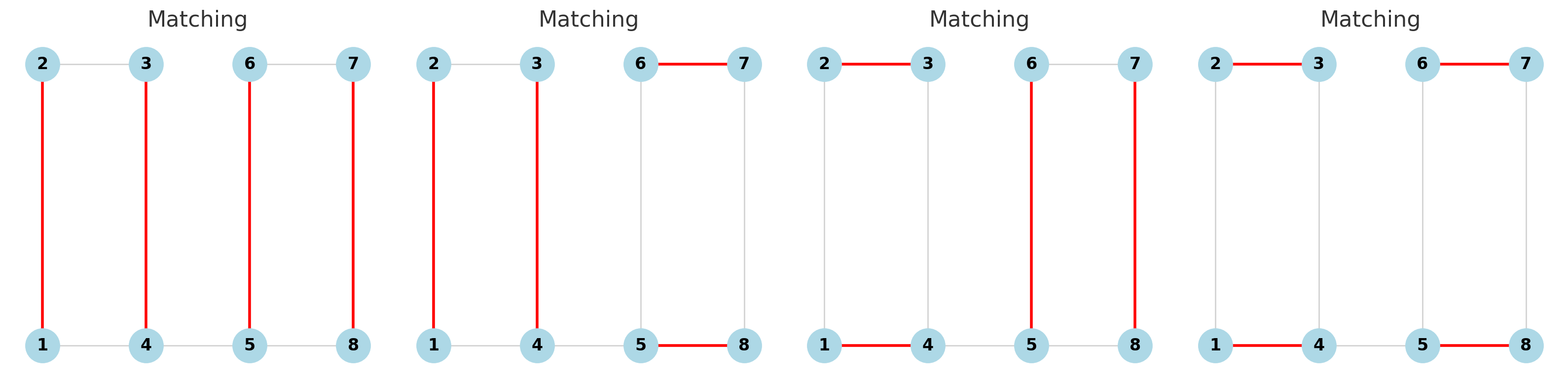
For example, for =8, all four matchings are shown in the image below: