Lucky Landing

Task

Two players, called Alunelu and Bocuțu, have luckily landed in Lucky Landing and have to loot the region.

We know that the path followed by each of the two players is a strictly convex polygon. Determine any two paths that the two players can follow such that they intersect in exactly $n$ points.

More formally, you are given a positive integer $n$.

Determine any two strictly convex polygons $A$ and $B$ which satisfy the following constraints:

• Both $A$ and $B$ must have between $3$ and $1 \ 000$ vertices.
• The vertices of both $A$ and $B$ must have integer coordinates which do not exceed $10^9$ in absolute value.
• There are exactly $n$ points which belong to both of the polygons' contours.

Input data

The first line of input contains a single integer $n$ ($3 \le n \le 100$) - the desired number of intersections between the two polygons.

Output data

On the first line, print the number of vertices $m$ ($3 \le m \le 1000$) of the first polygon.

On each of the next $m$ lines, print two integers $x_i$ and $y_i$ ($-10^9 \le x_i, y_i \le 10^9$) - the coordinates of the $i$-th vertex from the first polygon.

On the next line, print the number of vertices $p$ ($3 \le p \le 1000$) of the second polygon.

On each of the next $p$ lines, print two integers $a_i$ and $b_i$ ($-10^9 \le a_i, b_i \le 10^9$) - the coordinates of the $i$-th vertex from the second polygon.

Additionally, for each polygon:

• The points must be given in either clockwise or anti-clockwise order.
• No three consecutive points should be collinear.
• The points must, in the order they are given, be the vertices of a non-intersecting convex polygon.

Example 1

stdin

3

stdout

5
2 2
3 1
4 1
4 3
3 3
6
1 2
2 1
3 1
4 2
3 3
2 3

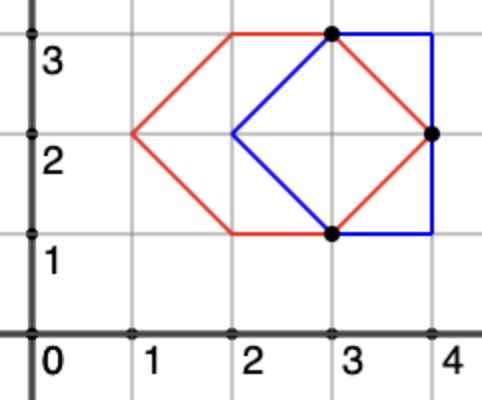
Explanation

The polygons from the first example are pictured as follows:

Example 2

stdin

4

stdout

4
1 1
1 5
5 5
5 1
3
1 1
7 3
3 7

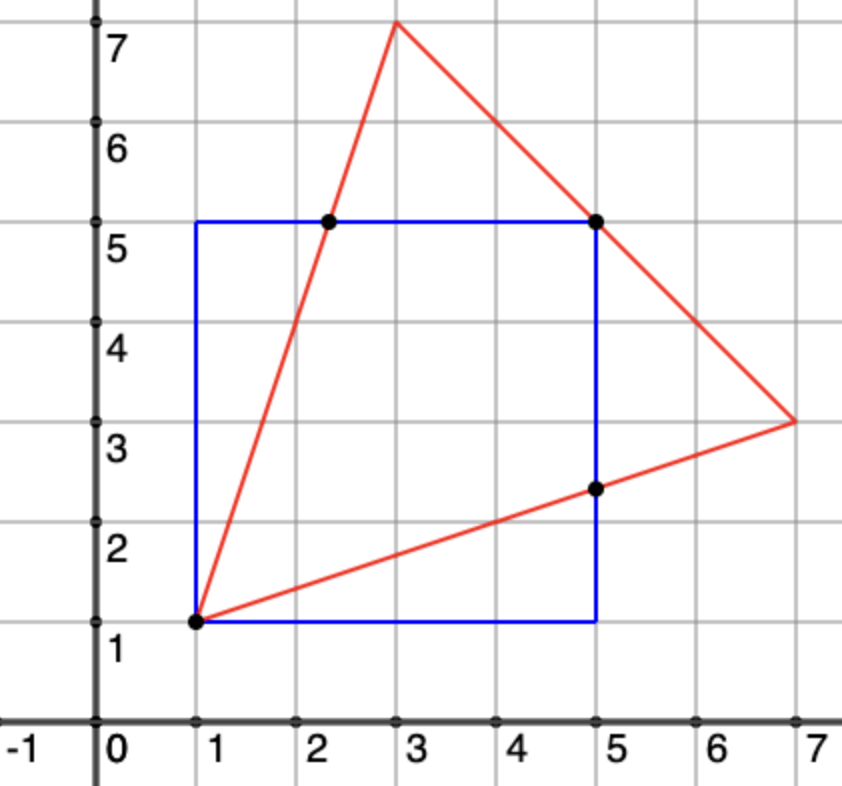
Explanation

The polygons from the second example are pictured as follows: