Mihai și Ioana au creat o reprezentare a matricii cu linii (numerotate de la la ) şi coloane (numerotate de la la ) în care fiecare element este determinat pe baza următoarei formule:
, unde și sunt indicii liniei și coloanei, iar este un număr natural nenul, ales de ei.
Se definesc următoarele categorii de numere:
- număr special: un număr natural de două cifre, al cărui pătrat este un număr de trei cifre, iar cifra zecilor din acest pătrat este egală cu suma dintre cifra sutelor și cifra unităților. Exemplu: este un număr special.
- număr aproape special: un număr care poate deveni special prin eliminarea a cel puțin unei cifre. Exemplu: este număr aproape special pentru că prin eliminarea cifrelor , și se obține numărul special .
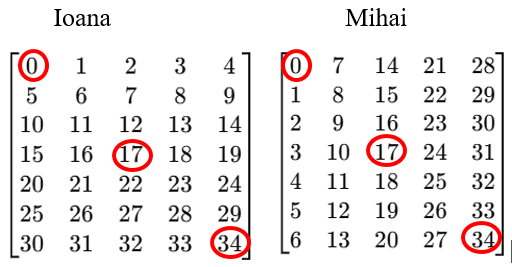
Mihai și Ioana încep, în același timp și cu aceeași viteză, explorarea matricii începând cu , folosind strategii diferite:
- Ioana se deplasează pe linii, de sus în jos, și pe fiecare linie de la stânga la dreapta.
- Mihai se deplasează pe coloane, de la stânga la dreapta, și pe fiecare coloană de sus în jos.
În anumite momente de timp, cei doi ajung simultan la același element.
Cerință
- Determinați numărul de numere speciale care există în matricea .
- Determinați numărul elementelor din matricea care sunt numere aproape speciale, la care Mihai și Ioana ajung în același timp.
Date de intrare
Fișierul de intrare special.in conține pe prima linie numărul natural , unde este cerința care trebuie rezolvată ( sau ). Pe a doua linie se află trei numere , separate prin câte un spațiu, cu semnificația din enunț.
Date de ieșire
Fișierul de ieșire special.out conține numărul determinat pentru cerința .
Restricții și precizări
| # | Scor | Restricții |
|---|---|---|
| 1 | 35 | , |
| 2 | 15 | , |
| 3 | 30 | , |
| 4 | 20 | , |
Exemplul 1
special.in
1
4 5 13
special.out
2
Explicație
. Se rezolvă cerința .
Matricea este
| 10 | 1 | 5 | 9 | 0 |
| 12 | 3 | 7 | 11 | 2 |
| 1 | 5 | 9 | 0 | 4 |
| 3 | 7 | 11 | 2 | 6 |
Numărul este special și apare de ori.
Exemplul 2
special.in
2
7 5 1000
special.out
1
Explicație
. Se rezolvă cerința .
Matricea este
| 25 | 29 | 33 | 37 | 41 |
| 40 | 44 | 48 | 52 | 56 |
| 55 | 59 | 63 | 67 | 71 |
| 70 | 74 | 78 | 82 | 86 |
| 85 | 89 | 93 | 97 | 101 |
| 100 | 104 | 108 | 112 | 116 |
| 115 | 119 | 123 | 127 | 131 |
Cei doi copii se întâlnesc la plecare în , apoi în și la sosire în .
În se află numărul care este aproape special.
Exemplul 3
special.in
2
11 21 3000
special.out
5
Explicație
. Se rezolvă cerința .
Sunt elemente ale matricii în care cei doi copii se întâlnesc, dintre care doar au ca valori numere aproape speciale.