Sile a învățat la ora de matematică definiția unui graf bipartit. Considerăm un graf neorientat format dintr-o mulțime de noduri și o mulțime de muchii . Spunem că este bipartit dacă și numai dacă există două submulțimi astfel încât:
- ;
- ;
- fiecare muchie din are o extremitate în și o extremitate în .
Sile a dat peste un graf neorientat , cu nodurile și muchiile , format din noduri () și muchii (). El se întreabă acum pentru care noduri avem că graful obținut prin eliminarea nodului și a muchiilor incidente lui din este bipartit.
Voi va trebui să îl ajutați pe Sile să își rezolve problema pentru scenarii.
Protocol de interacțiune
Concurentul trebuie să implementeze următoarea funcție, care va fi apelată pentru scenarii independente:
void solve(int N, int M, int* X, int* Y, char* S);
reprezintă numărul de noduri ale grafului, numărul de muchii ale grafului. și sunt două șiruri de lungime ce codifică mulțimea de muchii a grafului: pentru fiecare există o muchie între și . Concurentul trebuie să scrie răspunsul în șirul de lungime : pentru vom avea că 1 dacă graful este bipartit, și 0 altfel. Valorile scrise în sunt caractere, nu numere.
Restricții
- Nu vor exista muchii cu .
- Nu vor exista muchii care să apară de mai multe ori în cadrul aceluiași scenariu.
- Se consideră identice muchiile și .
Subtask 1 (23 puncte)
- Suma valorilor nu va depăși .
- Suma valorilor nu va depăși .
Subtask 2 (32 puncte)
- Suma valorilor nu va depăși .
- Suma valorilor nu va depăși .
- Se acordă punctaj complet oricărei surse care găsește răspunsul corect cel puțin pentru nodurile pentru care există maxim două muchii incidente în . Cu toate acestea, se cere ca valorile să fie mereu
0sau1pentru .
Subtask 3 (22 puncte)
- Suma valorilor nu va depăși .
- Suma valorilor nu va depăși .
Subtask 4 (23 puncte)
- Suma valorilor nu va depăși .
- Suma valorilor nu va depăși .
Exemplu
| Apelurile comisiei | Efect |
|---|---|
solve(4, 3, {1,1,2}, {2,3,3}, S) |
1110 |
solve(6, 7, {1,1,2,2,4,4,5}, {2,3,3,4,5,6,6}, S) |
000000 |
Explicație
Avem scenarii de rezolvat.
În primul scenariu graful este cel din imaginea de mai jos.
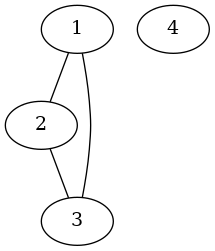
Observăm că nodurile , și sunt vecine două câte două, de unde deducem că graful nu este bipartit. Prin eliminarea oricăruia dintre nodurile , sau , graful rezultat va fi bipartit. De exemplu, dacă am elimina nodul (implicit și muchiile sale incidente și ), atunci graful rezultat va fi bipartit, deoarece se pot alege submulțimile și respectând proprietățile din enunț (n.b. există și alte modalități de a alege mulțimile , ). Eliminarea nodului nu ar duce la un graf bipartit. Așadar, răspunsul pentru acest scenariu este 1110.
În al doilea scenariu graful este cel din imaginea de mai jos.
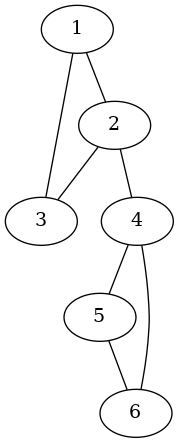
În acest caz, indiferent ce nod s-ar elimina din , graful rezultat nu ar fi bipartit. Așadar, răspunsul în acest caz este 000000.