Mugurița

Gâsca Rugum cea Malefică a răpit-o pe Prințesa Mugurița, iar Imperiul Rațelor de Cauciuc se află într-o criză fără precedent. Prințul Mugurel a fost trimis în misiune pentru a-și salva dragostea de la captivitatea etrnă. Echipajul Spionilor M.A.C. îl teleportează pe Mugurel în centrul unui labirint infinit, în camera de coordonate $(0,0)$.

Spionând cu drona deasupra labirintului, ei observă că acesta este format din camere hexagonale, iar din fiecare cameră Mugurel se poate deplasa cu un singur pas într-o cameră vecină.

Sistemul de coordonate este însă unul neobișnuit. Din camera de coordonate $(i, j)$ se poate merge cu un singur pas în oricare dintre camerele $(i − 1, j + 2)$, $(i + 1, j + 2)$, $(i + 2, j)$, $(i + 1, j − 2)$, $(i − 1, j − 2)$, $(i − 2, j)$.

Datorită dimensiunii infinite a labirintului, echipajul adoptă strategia Trandafirul. Prin această strategie, Mugurel va parcurge labirintul în spirală, mergând inițial în camera din dreapta-sus, apoi în sensul invers al acelor de ceasornic.

De exemplu, după $15$ pași (considerând că la pasul $0$ se află în camera inițială), traseul lui Mugurel va fi:
$(0, 0) \rightarrow (1, 2) \rightarrow (−1, 2) \rightarrow (−2, 0) \rightarrow (−1, −2) \rightarrow (1, −2) \rightarrow (2, 0) \rightarrow (3, 2) \rightarrow (2, 4) \rightarrow (0, 4) \rightarrow (−2, 4) \rightarrow (−3, 2) \rightarrow (−4, 0) \rightarrow (−3, −2) \rightarrow (−2, 4) \rightarrow (0, −4)$

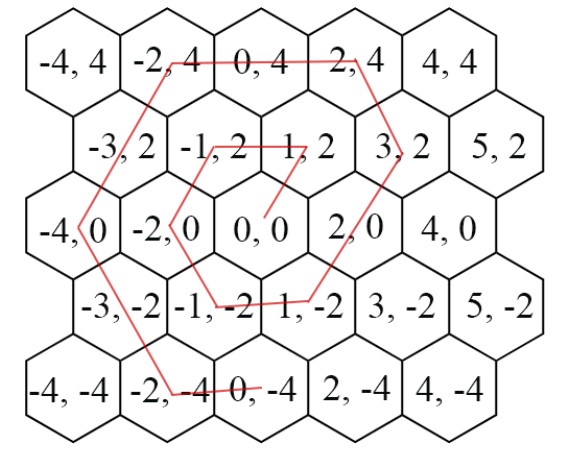
Zburând cu drona deasupra labirintului, echipajul reușește să găsească într-un final prințesa:

”Mugurel, am găsit prințesa! Grăbește-te, folosește transportatorul pentru a te deplasa spre ea și salveaz-o! A, cum se calibrează aceasta? Simplu, trebuie să introduci..." - conexiunea se întrerupe înainte să poată auzi ultimele instrucțiuni.

Transportatorul are nevoie de două calibrări, ambele folosind strategia Trandafirul:

1. Dându-se un număr de pași $Z$, precizați coordonatele camerei în care se ajunge după efectuarea acestora.
2. Dându-se coordonatele $(X, Y)$ ale unei camere, precizați după câți pași se ajunge acolo.

Ajutați-l pe Mugurel să calibreze dispozitivul și să salveze prințesa!

Date de intrare

Prima linie va conține un număr $C$, reprezentând tipul calibrării.
Dacă $C = 1$, atunci a doua linie va conține un singur număr $Z$, reprezentând numărul de pași efectuați.
Dacă $C = 2$, atunci a doua linie va conține două numere întregi $X și Y$, reprezentând coordonatele camerei în care trebuie ajuns.

Date de ieșire

Dacă $C = 1$, atunci prima linie va conține două numere $A$ și $B$, reprezentând răspunsul la prima calibrare - coordonatele camerei în care se ajunge după $Z$ pași.
Dacă $C = 2$, atunci prima linie va conține un singur număr $K$, reprezentând răspunsul la a doua calibrare - după câți pași se ajunge în camera de coordonate $(X, Y)$.

Restricții și precizări

• $C \in {1, 2}$
• $−10^9 \leq X, Y \leq 10^9$
• $0 \leq Z \leq 10^{18}$
• Se garantează că $X$ și $Y$ sunt coordonate valide ale unei camere din labirint.

Exemplul 1

mugurita.in

1
4

mugurita.out

-1 -2

Explicație

În primul exemplu, observăm pe traseul din exemplu că după $4$ pași ajungem în căsuța de coordonate $(-1,-2)$.

Exemplul 2

mugurita.in

2
0 -4

mugurita.out

15

Explicație

În al doilea exemplu, căsuța de la coordonatele $(0,-4)$ este chiar cea din exemplul din enunț, în care se ajunge după $15$ pași.

Exemplul 3

mugurita.in

2
180 400

mugurita.out

119610

Explicație

În al treilea exemplu, în căsuța de coordonate $(180, 300)$ se intră după $119 \ 610$.